Eubrewnet Wiki
Eubrewnet Documentation
Eubrewnet Documentation
AEMET Report 20201115
S5P Mission Performance Centre
Eubrewnet Uncertainty Budget- WP1 Instrumental parameters
prepared by Alberto Reodondas, Francisco Parra-Rojas, Javier López-Solano and Alberto Berjón
In this document we present the uncertainty estimation of the total ozone measured by the Brewer spectrophotometers focusing on the instrumental parameters. The uncertainty model was developed during the ATMOZ project. This model describe the uncertainty model reference instruments: that is the instruments that are absolutely calibrated by Langley method (Redondas et al., 2014a) at the conditions of the 2016 ATMOZ campaign refered as IZO16 (Cuevas et al., 2015). The objective of the project is to extend this model to network instruments of the using the observations stored at EUBREWNET (Anon, n.d.a; Anon, n.d.b).
On this report we summarize the developments of the first step which is focused on the instrumental parameters that affect the model, considering the Langley calibration and the calibration transfer to the network instruments.
For calibration of sun photometers instruments like the Brewer spectrometer the extraterrestrial constants need to be known (i.e. intensity of the radiation outside the atmosphere at the required wavelengths). This concept requires constant total ozone amount at clean sites, which is difficult to ensure for extratropical sites, because changes in synoptic meteorological condition can lead to changes in column ozone amount (e.g. (Dobson and Normand, 1958)). This problem is much less severe in remote (clean) sites in the tropics (or subtropics), and it is therefore more adequate to perform absolute calibration at such sites.One of this places is the Izaña Atmospheric Research Centre located at the Izaña mountain at 2367 m.a.s.l. on the Tenerife island were Regional Brewer Calibration Center were establish in 2003. RBCC-E owns a full calibration and reference-maintenance equipment composed by three Brewer spectrometers (The IZO Triad): a Regional Primary Reference (Brewer 157), a Regional Secondary Reference (Brewer 183) and a Regional Travelling Reference (Brewer 185). Brewer inter-comparisons are held annually, alternating between Arosa in Switzerland and the El Arenosillo Sounding Station of the Instituto Nacional de Técnica Aeroespacial (INTA) at Huelva in the south of Spain. The reference transferred to the campaigns is the mean of the three independently calibrated Brewer instruments.
The methodology of the calibration can be summarized in three steps:
The points 1 and 2 of this methodology were tested and validated with the cooperation of Metrology Institutes during the ATMOZ project, in which the RBCC-E participated together with the Dobson World and Brewer European Calibration Centres. The methodology used is described in (Ito et al., 2014; Redondas, 2003; Redondas et al., 2018a). The calibration transfer to the network instrument is performed during the intercomparison campaigns which methodology is summarized in Redondas et al. (2018a)
The next pages are organized as follows. In Sec.2, we describe the Brewer uncertainty model developed during the ATMOZ (???) project. The application to reference instrument during the ATMOZ campaign are summarized on section 3 and the results when we apply to network instruments are shown in section 4. The model allow us determine the relative importance of the instrumental parameters on section 5 and finally determine the the parameters that to be include on the Eubrewnet database (Sect 6).
The overall uncertainty of total ozone column is composed by the instrumental measurement uncertainties and the retrieval model uncertainties, and their interactions. This section presents first, the method to address the overall uncertainty from the Brewers measurements and retrieval algorithms, based on cross-correlation matrices.
TOC measurements performed by Brewer instruments are made by measuring the relative intensities of UV radiation reaching the Earth’s surface at a set of six wavelengths, which are 303.2 nm (Hg slit), 306.3 nm (SO ), 310.1 nm, 313.5 nm, 316.8 nm and 320.1 nm within the O
), 310.1 nm, 313.5 nm, 316.8 nm and 320.1 nm within the O community. The O
community. The O measurement equation is based on the Beer-Lambert law, which reads
measurement equation is based on the Beer-Lambert law, which reads
![Equation $$\label{eq1}
I_{\lambda} = I_{0\lambda}\exp\left[ -\alpha_{\lambda} \mu \Omega - \beta_{\lambda}m\frac{p}{p_{0}} - \delta_{\lambda}\sec(Z)\right]$$](/dokuwiki/lib/exe/fetch.php?media=wiki:latex:/img70c2bfe8e2f3c87a2bc99b8045236f20.png)
where
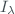 is the direct normal spectral irradiance at wavelength
is the direct normal spectral irradiance at wavelength  , expressed in
, expressed in 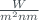 .
.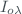 is the extraterrestrial spectral irradiance at wavelength
is the extraterrestrial spectral irradiance at wavelength  , expressed in
, expressed in 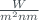 .
.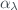 is the ozone absorption coefficient at wavelength
is the ozone absorption coefficient at wavelength  , in
, in 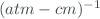 .
.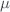 is the ratio of actual and vertical paths of solar radiation through the ozone layer.
is the ratio of actual and vertical paths of solar radiation through the ozone layer.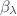 is the Rayleigh scattering coefficient at wavelength
is the Rayleigh scattering coefficient at wavelength  , in
, in  .
. is the airmass corresponding to solar zenith angle.
is the airmass corresponding to solar zenith angle.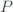 is the atmospheric pressure at the measurement station, in
is the atmospheric pressure at the measurement station, in 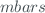 .
.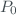 is the mean sea pressure, in
is the mean sea pressure, in 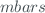 .
.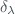 is the scattering coefficient (optical depth) of aerosol at wavelength
is the scattering coefficient (optical depth) of aerosol at wavelength  .
.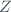 is the solar zenith angle, in
is the solar zenith angle, in 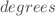 .
. is the TOC in Dobson units,
is the TOC in Dobson units,  , which is the variable of observation.
, which is the variable of observation.The measured signal can be written as
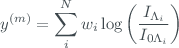
where are Brewer weighting coefficients at the different wavelengths selected to verify 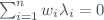 . The model to be matched with these measured data is
. The model to be matched with these measured data is
![Equation $$\label{eq3}
y = -\sum_{i}^{N} w_{i} \left[\alpha_{\lambda_{i}} \mu \Omega - \beta_{\lambda_{i}}m\frac{p}{p_{0}} - \delta_{\lambda_{i}}\sec(Z)\right]$$](/dokuwiki/lib/exe/fetch.php?media=wiki:latex:/imgc38a8d077ed1204b108a16cecd6edc19.png)
This model can be simplified by setting
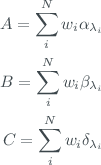
So that equation ([eq3]) becomes
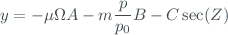
and then

A definite advantage of equation ([eq5]) (which in metrology is usually called the 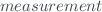
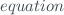 ) comes from its linearity and, as consequence, its ability of directly providing TOC values, without resorting to sophisticated inversion algorithms. To what concerns the uncertainty associated to TOC measurements, it is convenient to first divide the sources of uncertainties in distinct classes, such as:
) comes from its linearity and, as consequence, its ability of directly providing TOC values, without resorting to sophisticated inversion algorithms. To what concerns the uncertainty associated to TOC measurements, it is convenient to first divide the sources of uncertainties in distinct classes, such as:
In practice, instead of determining  by minimizing the difference between equations ([eq2]) and ([eq4]), as common for non linear models, in this case
by minimizing the difference between equations ([eq2]) and ([eq4]), as common for non linear models, in this case  can be directly obtained by inverting the equation
can be directly obtained by inverting the equation 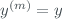 . However, for the determination of the measurement uncertainty coming from the model, and the related cross-correlations, one can still pass through minimizing the distance, according to some specific metric, between
. However, for the determination of the measurement uncertainty coming from the model, and the related cross-correlations, one can still pass through minimizing the distance, according to some specific metric, between 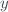 and
and 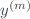 . For the sake of generality, let us represent
. For the sake of generality, let us represent 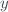 as in the following
as in the following
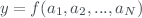
where 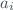 is the
is the  -
-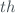 influence parameter, and
influence parameter, and 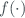 is the function describing the dependency of the measured quantities on them.
is the function describing the dependency of the measured quantities on them.
To test the Brewer uncertainty model we have used two different data sets. The first data set is the Standard Algorithm used by Brewer in which include, among others, the cross sections of Bass and Paur (1985), a constant effective height of 22 km for the ozone layer or the coefficients of Rayleigh scattering provided by Bates (1984) which have a uncertainty of 1%. The second data set is called Algorithm V2 in which changes have been made in the atmospheric parameters and the model. In this case the absorption cross sections selected is from Gorshelev et al. (2014) and Serdyuchenko et al. (2013), effective heights and effective temperature and are not considered constant and Rayleigh scattering coefficients are provided by Nicolet (1984) with an uncertainty of 0.5%, among others. These parameters are shown in Table [table_var].
To obtain a correct value of the TOC uncertainty budget of the Brewer spectrophotometers, the steps recommended in (Guides in Metrology, 2008) have been followed. The typical uncertainty of 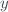 , where
, where 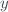 is the result of the measurement (regarding the measurand
is the result of the measurement (regarding the measurand 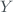 ), is obtained by adequately composing the typical uncertainties of the input estimates
), is obtained by adequately composing the typical uncertainties of the input estimates 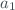 ,
, 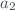 ,…,
,…,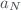 . This combined standard uncertainty of the estimate
. This combined standard uncertainty of the estimate 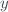 and denotes
and denotes 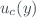 .
.
The combined standard uncertainty 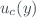 is the positive root of the combined variance
is the positive root of the combined variance 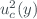 , given by
, given by
![Equation $$\label{eq7}
u_{c}^{2}(y) = \sum_{i=1}^{N}\left[ \frac{\partial f}{\partial a_{i}} \right]^{2} u^{2}(a_{i})$$](/dokuwiki/lib/exe/fetch.php?media=wiki:latex:/imgd0718c053395e56e9629dd9a39928ee6.png)
where 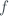 is the function given in equation ([eq6]). Each
is the function given in equation ([eq6]). Each 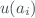 is a standard uncertainty evaluated as type A or type B. Type A evaluation of standard uncertainty is associated to an input estimate obtained from statistical analysis of a set of observations, while if we obtain it by other non-statistical mechanisms we are talking about type B evaluation of standard uncertainty. The combined standard uncertainty
is a standard uncertainty evaluated as type A or type B. Type A evaluation of standard uncertainty is associated to an input estimate obtained from statistical analysis of a set of observations, while if we obtain it by other non-statistical mechanisms we are talking about type B evaluation of standard uncertainty. The combined standard uncertainty 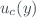 is an estimated standard deviation and characterizes the dispersion of the values that could be reasonably attributed to the measurand
is an estimated standard deviation and characterizes the dispersion of the values that could be reasonably attributed to the measurand 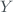 .
.
Equation ([eq7]) and its equivalent for the correlated input quantities (Eq. ([eq8])) based both on a first order Taylor series expansion of equation ([eq6]) express the Law of Uncertainty Propagation.
When the input quantities are correlated, the appropriate expression for the combined variance 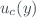 associated with the measurement result is
associated with the measurement result is
![Equation $$\label{eq8}
u_{c}^{2}(y) = \sum_{i=1}^{N} \left[ \frac{\partial f}{\partial a_{i}} \right]^{2} u^{2}(a_{i}) + 2\sum_{i=1}^{N-1}\sum_{j=i+1}^{N} \frac{\partial f}{\partial a_{i}}\frac{\partial f}{\partial a_{j}}u(a_{i},a_{j})$$](/dokuwiki/lib/exe/fetch.php?media=wiki:latex:/img8d19bda0fab13450864737ef9a902284.png)
where 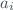 and
and 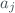 are the estimates of
are the estimates of  and
and 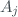 and
and 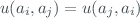 is the estimated covariance associated with
is the estimated covariance associated with 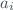 and
and 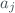 or cross correlation matrix
or cross correlation matrix 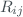 . The degree of correlation between
. The degree of correlation between 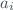 and
and 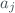 is given by the estimated correlation coefficient
is given by the estimated correlation coefficient
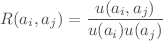
where 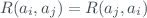 and
and  .
.
Solving the estimated covariance associated with 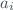 and
and 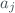 in equation ([eq9]) and substituting in equation ([eq8]), we obtain
in equation ([eq9]) and substituting in equation ([eq8]), we obtain
![Equation $$\label{eq10}
u_{c}^{2}(y) = \sum_{i=1}^{N} \left[ \frac{\partial f}{\partial a_{i}} \right]^{2} u^{2}(a_{i}) + 2\sum_{i=1}^{N-1}\sum_{j=i+1}^{N} \frac{\partial f}{\partial a_{i}}\frac{\partial f}{\partial a_{j}}u(a_{i})u(a_{j})R(a_{i},a_{j})$$](/dokuwiki/lib/exe/fetch.php?media=wiki:latex:/img2a4090066711785b89ca76b52bd07170.png)
If the estimations 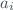 and
and 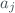 are independent,
are independent, 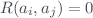 and we get again the equation ([eq7]).
and we get again the equation ([eq7]).
In our case the estimated covariances can be found by inverting the associated Jacobian matrix which can be obtained as
![Equation $$\label{eq11}
J_{ij} = \left[ \frac{\partial f}{\partial a_{i}} \cdot \frac{\partial f}{\partial a_{j}} \right]$$](/dokuwiki/lib/exe/fetch.php?media=wiki:latex:/imgdab12575a429c85adb19dbad93a25c3d.png)
which is clearly symmetrical 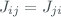 .
.
This situation would be possible, of course, if the Jacobian matrix were not singular or ill-conditioned. Unfortunately this is not the case for our model. In order to be able to compute the inverse of the Jacobian matrix and provide an estimate of the degrees of cross correlation, we need to use numerical techniques such as the Levenberg-Marquardt algorithm 1).
Applying the equation ([eq10]) to the Brewer TOC model shown in equation ([eq4]), we obtain a quadratic  -dependent equation
-dependent equation
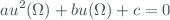
where
![Equation $$\begin{gathered}
a = \left(\frac{\partial y}{\partial \Omega}\right)^{2} \\[10pt]
b = 2 \frac{\partial y}{\partial \Omega} \left[ \sum_{i=1}^{N-1} \frac{\partial y}{\partial a_{i}} u(a_{i})R(\Omega,a_{i}) \right] \\[10pt]
c = \sum_{i=1}^{N-1} \left(\frac{\partial y}{\partial a_{i}}\right)^{2}u^{2}(a_{i}) + 2\sum_{i=1}^{N-2}\sum_{j=i+1}^{N-1}\left( \frac{\partial y}{\partial a_{i}} \right)\left( \frac{\partial y}{\partial a_{j}} \right)u(a_{i})u(a_{j})R(a_{i},a_{j}) - u^{2}(y)\end{gathered}$$](/dokuwiki/lib/exe/fetch.php?media=wiki:latex:/img40a92ab5ba19a2eea43bb933a46b3daf.png)
The overall TOC uncertainty budget can be estimated through two main components: the measurement uncertainties for the Brewer spectrophotometer and the uncertainties that come from the atmospheric model. The measurement uncertainties are derived from the noise of the signal and the instrumental corrections (dead time, temperature, neutral filters,…). The signal recorded by the Brewer must be corrected of the instrumental characteristics to get an accurate value of the ozone amount. The Brewer spectrophotometer measures the solar radiation in five operational wavelengths (306.3 nm, 310.1 nm, 313.5 nm, 316.8 nm and 320.1 nm) and a dark current. These irradiances are recorded by the spectrophotometer in raw-counts (counts per integration time) and must be converted in count-rates (counts per second) as follows
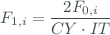
where 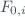 are the raw-counts at each slit and
are the raw-counts at each slit and 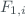 the count-rates for each slit
the count-rates for each slit  [s
[s ],
], 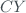 is the number of the slit mask cycles (usually =20) and
is the number of the slit mask cycles (usually =20) and  is the integration time (=0.1147 s) of the photomultiplier. At the same way, the dark signal (
is the integration time (=0.1147 s) of the photomultiplier. At the same way, the dark signal ( ) must be converted in count rates. The uncertainty associated to the raw-counts to count-rates conversion is
) must be converted in count rates. The uncertainty associated to the raw-counts to count-rates conversion is

We also need to apply the dark count correction on the data as

and assuming independent variables, the uncertainty of 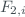 is given by
is given by
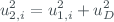
where 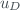 is the standard deviation of the dark counts. The dead time is a measurement of the time in which two consecutive photons can be detect by the photomultiplier and its value is obtained through routine calibrations. Assuming a Poisson statistic for the signal, the count-rates after the dead time correction are
is the standard deviation of the dark counts. The dead time is a measurement of the time in which two consecutive photons can be detect by the photomultiplier and its value is obtained through routine calibrations. Assuming a Poisson statistic for the signal, the count-rates after the dead time correction are
![Equation $$\label{dt_corr}
F_{3,i} = F_{2,i}\exp[\tau F_{3,i}]$$](/dokuwiki/lib/exe/fetch.php?media=wiki:latex:/imgc7bf996bf5a3934125f6a609dbea9768.png)
where  is the dead time. To get a more accurate value of
is the dead time. To get a more accurate value of 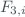 is necessary to run at least nine iterations in the previous calculation (Fountoulakis et al., 2016). The expanded uncertainty associated with the dead time correction is then given as
is necessary to run at least nine iterations in the previous calculation (Fountoulakis et al., 2016). The expanded uncertainty associated with the dead time correction is then given as
![Equation $$\label{dt_unc}
u_{3,i}^{2} = \left(\frac{\exp[\tau F_{3,i}]}{1 - \tau F_{3,i}}\right)^{2}u_{2,i}^{2} + F_{3,i}^{4}u_{\tau}^{2}$$](/dokuwiki/lib/exe/fetch.php?media=wiki:latex:/imgb9abb1d58bd1362b5859dd20ce845467.png)
where the dead time uncertainty 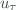 (=1 ns) was obtained in a previous work of Fountoulakis et al. (2016). The dead time-corrected count-rates and their uncertainties are normalized by computing the base ten logarithmic and thus allowing integer arithmetic
(=1 ns) was obtained in a previous work of Fountoulakis et al. (2016). The dead time-corrected count-rates and their uncertainties are normalized by computing the base ten logarithmic and thus allowing integer arithmetic
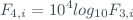
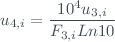
The count-rates also must be corrected of the absolute temperature of the photomultiplier. The temperature of the observatory ( ) oscillated between 18ºC and 28ºC during the campaign. With these temperature values and with the temperature coefficients for each slit (
) oscillated between 18ºC and 28ºC during the campaign. With these temperature values and with the temperature coefficients for each slit ( ) obtained through previous calibrations, we can get the absolute temperature correction as
) obtained through previous calibrations, we can get the absolute temperature correction as
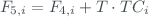
The uncertainty of 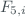 is given by
is given by

where 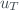 is the temperature uncertainty due to the photomultiplier temperature resolution (1ºC) and
is the temperature uncertainty due to the photomultiplier temperature resolution (1ºC) and 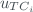 are the uncertainties of the temperature coefficients for each slit.
are the uncertainties of the temperature coefficients for each slit.
Once these instrumental corrections have been done, we can carry out a double ratio (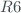 ) with the Brewer weighting coefficients at the different wavelengths
) with the Brewer weighting coefficients at the different wavelengths

and in a similar way with the relative uncertainties of the corrected count-rates (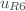 ).
).
To obtain a correct value of the measurement parameter, it is necessary to apply one last instrumental corrections. One related to the non-linearity of 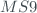 with neutral filters and the other one to the variation of
with neutral filters and the other one to the variation of 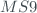 with wavelength. The
with wavelength. The 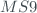 variable is defined as the double-ratio
variable is defined as the double-ratio 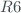 corrected by the Rayleigh scattering
corrected by the Rayleigh scattering
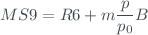
which includes non-instrumental parameters. Since for the correct calculation of the ozone overall uncertainty we must separate the instrumental parameters from the non-instrumental, applying this correction directly to 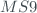 would not be feasible. However, and due to the linearity of
would not be feasible. However, and due to the linearity of 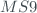 , this correction can be applied to
, this correction can be applied to 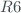 and then correct for Rayleigh scattering with a negligible error probably related to computational rounding. Therefore, we first apply the correction due to the non-linearity of the neutral filters with the wavelength that would be
and then correct for Rayleigh scattering with a negligible error probably related to computational rounding. Therefore, we first apply the correction due to the non-linearity of the neutral filters with the wavelength that would be

and the uncertainty of the correction is
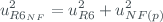
where 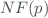 is the non-linearity coefficient of each filter position
is the non-linearity coefficient of each filter position  and
and  its uncertainty.
its uncertainty.
Finally, a uncertainty related with variation of 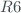 with the wavelength must be done. The ozone vs. wavelength (step number) follows an ideal parabola with the maximum in the ozone reference position, this measurement called Sun Scan is routinely performed and is used to determine the optimal wavelength of the spectrometer (Sun Scan Reference). We can use this measurement to estimate the error in the double ratio when the measure is done outside of the reference wavelengths. We have estimate the percentage variation of the double ration
with the wavelength must be done. The ozone vs. wavelength (step number) follows an ideal parabola with the maximum in the ozone reference position, this measurement called Sun Scan is routinely performed and is used to determine the optimal wavelength of the spectrometer (Sun Scan Reference). We can use this measurement to estimate the error in the double ratio when the measure is done outside of the reference wavelengths. We have estimate the percentage variation of the double ration 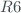 with the slope of the fit against wavelength.
with the slope of the fit against wavelength.
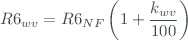
where  is the slope of the linear fit and its uncertainty is given by
is the slope of the linear fit and its uncertainty is given by

being  the uncertainty of the slope. The final product of the ozone is a mean of five consecutive measurements (in the case of the optical masses is the median) and with this, the uncertainty of the total column ozone can be reduced.
the uncertainty of the slope. The final product of the ozone is a mean of five consecutive measurements (in the case of the optical masses is the median) and with this, the uncertainty of the total column ozone can be reduced.
The optical masses of both the ozone layer (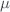 ) and the Rayleigh scattering layer (
) and the Rayleigh scattering layer ( ) depend on the SZA and their respective effective heights (
) depend on the SZA and their respective effective heights (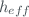 ).
).
![Equation $$\label{opmas}
\mu = \sec\left[\arcsin \left(\frac{R_{\Earth}}{R_{\Earth} + h_{eff}}\sin(SZA) \right) \right]$$](/dokuwiki/lib/exe/fetch.php?media=wiki:latex:/imgcbd70c4951957792b2008eaf430e7f3a.png)
where 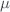 (or
(or  for the Rayleigh scattering layer) is the ozone optical mass,
for the Rayleigh scattering layer) is the ozone optical mass, 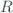 is the Earth radius and
is the Earth radius and 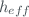 is the effective altitude of the ozone (or Rayleigh scattering) layer.
is the effective altitude of the ozone (or Rayleigh scattering) layer.
We have also include in atmospheric parameters the effective temperature 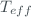 of the ozone layer needed to estimate the ozone absorption coefficient uncertainty and the pressure of the observatory which is part of the Rayleigh scattering component in equation ([eq5]).
of the ozone layer needed to estimate the ozone absorption coefficient uncertainty and the pressure of the observatory which is part of the Rayleigh scattering component in equation ([eq5]).
We define model parameters those that do not depend, or at least not totally, on atmospheric factors. In the case of the algorithm for obtaining TOC and its uncertainty, these are: the ozone absorption coefficients (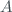 ), the Rayleigh dispersion coefficients (
), the Rayleigh dispersion coefficients (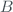 ) and the ETC.
) and the ETC.
The ozone absorption coefficient is calculated through the expression
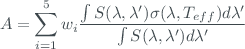
where 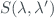 is the slit function (isosceles triangle truncated to 0.87) centered on the wavelength of each slit (
is the slit function (isosceles triangle truncated to 0.87) centered on the wavelength of each slit ( ) and with a defined FWHM, and
) and with a defined FWHM, and  is the cross section at an effective temperature (
is the cross section at an effective temperature (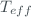 ) for each wavelength. We have differentiated 4 sources of uncertainty that must be analyzed separately and added in quadrature sum.
) for each wavelength. We have differentiated 4 sources of uncertainty that must be analyzed separately and added in quadrature sum.
These are: the uncertainty of the cross section (equation ([bicuad])), the uncertainty of the integration method, that corresponding to the variation of the absorption coefficient with temperature and its variation with the wavelength. These uncertainties are summed in quadrature.
The first one is the one corresponding to the error of the cross section that can be expressed as a bi-quadratic function of the temperature (Weber et al., 2016)
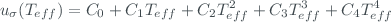
both the coefficients and the effective temperature of the ozone layer depend on the used algorithm.
The effect of the effective temperature will be studied in detail on the next report who deal to the atmospheric parameters.
Two sets of data have been used for the Rayleigh scattering coefficients ( ), one for each algorithm. For the standard algorithm, those provided by Bates (1984) have been used for each wavelength, which assigns an error of 1% in these coefficients. On the other hand, for the Rayleigh scattering coefficients corresponding to the V2 algorithm, those provided by Nicolet (1984) have been used, which have been calculated using the wavelength dispersion of each Brewer. Nicolet (1984) assigns a 0.5% error to these Rayleigh scattering coefficients.
), one for each algorithm. For the standard algorithm, those provided by Bates (1984) have been used for each wavelength, which assigns an error of 1% in these coefficients. On the other hand, for the Rayleigh scattering coefficients corresponding to the V2 algorithm, those provided by Nicolet (1984) have been used, which have been calculated using the wavelength dispersion of each Brewer. Nicolet (1984) assigns a 0.5% error to these Rayleigh scattering coefficients.
Last but not least, we have also obtained the extraterrestrial constant (ETC) and its respective uncertainties. In this case, and for both algorithms, three different methods have been used. For the reference Brewer (185) the Langley calibration has been used through the Beer-Lambert Law and carrying out a linear adjustment between 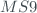 and
and 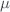 . We can obtain the value of ETC as the one where the line intersects the ordinate axis.
. We can obtain the value of ETC as the one where the line intersects the ordinate axis.
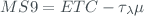
The uncertainties of the ETC by the Langley method have been obtained using, on the one hand, the uncertainties in 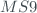 and
and 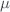 applying the York method 2)) which provides us with a systematic error, and on the other hand the standard deviation of the different ordinates at the origin obtained for the days of the campaign (random error). For Brewer 183 we have used the calibration transfer from brewer 185 with the 1-Point method in which we only obtain the ETC value, and the uncertainty is obtained by propagation of errors and a statistical uncertainty obtained from the standard deviation of the ETC measurements. However, in order to carry out the calibration transfer, it is necessary to synchronize both brewers at 5 minutes in time and at 1% in SZA.
applying the York method 2)) which provides us with a systematic error, and on the other hand the standard deviation of the different ordinates at the origin obtained for the days of the campaign (random error). For Brewer 183 we have used the calibration transfer from brewer 185 with the 1-Point method in which we only obtain the ETC value, and the uncertainty is obtained by propagation of errors and a statistical uncertainty obtained from the standard deviation of the ETC measurements. However, in order to carry out the calibration transfer, it is necessary to synchronize both brewers at 5 minutes in time and at 1% in SZA.
The Langley method is used to calibrate reference instruments. The Beer-Lambert Law is used to estimate ozone through a linear fit, the extraterrestrial constant for the instrument in question assuming constant ozone during the experiment León-Luis et al. (2018). Performing the optical mass of ozone 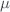 on the X axis and the double ratio
on the X axis and the double ratio 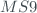 on the Y axis, and making a linear least squares fit, we can estimate the ETC as the cut of the line on the ordinate axis. The slope of the line will be
on the Y axis, and making a linear least squares fit, we can estimate the ETC as the cut of the line on the ordinate axis. The slope of the line will be 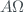 . To calculate the uncertainty of the ETC calculation, the York method 3) has been used, making use of the uncertainties inherent to the optical mass of ozone and the double ratio
. To calculate the uncertainty of the ETC calculation, the York method 3) has been used, making use of the uncertainties inherent to the optical mass of ozone and the double ratio 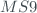 . Obviously, the total uncertainty of the
. Obviously, the total uncertainty of the 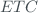 obtained by the Langley method is not only that provided in the adjustment coefficients. At this Type B uncertainty, the uncertainty (standard deviation) associated with the statistical sample (Type A) used to perform this calculation must be added in quadrature.
obtained by the Langley method is not only that provided in the adjustment coefficients. At this Type B uncertainty, the uncertainty (standard deviation) associated with the statistical sample (Type A) used to perform this calculation must be added in quadrature.

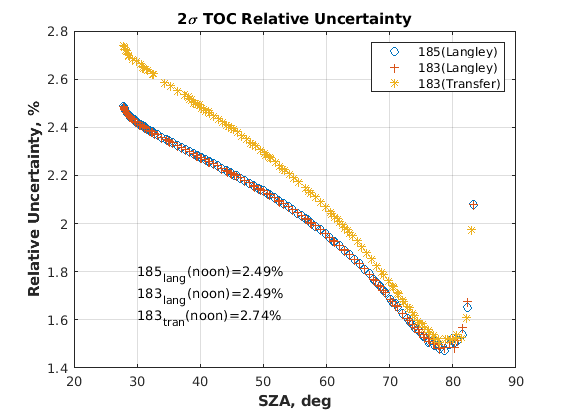
Type A uncertainty for Langley’s calculation for the Brewer 185 using data from the IZO16 campaign is barely distinguishable from the algorithm employed. This is due to the fact that the values of both the MS9 and its uncertainty only depend on instrumental parameters which do not depend on the algorithm. And the dependence of the optical mass of ozone with the algorithm used is only present in the effective height of the ozone layer and as it will be seen later, its contribution is only significant at high zenith angles, which are not are often used for this method.
The type A error estimation of the Langley at IZO16 is estimated as 10 ETC units whereas the type B is much lower (1.6 ETC units).
The methodology of the network instruments is done by comparison with a reference instrument (Redondas et al., 2018b), using simultaneous measurements. We use the ozone data from the reference instrument, synchronized in time (5 min) with the measurements calibrated instruments. The measurements are also synchronized with the zenith angle such that both measurements differ by less than 1% in 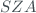 . So, through the equation
. So, through the equation

For every synchronized measurement we can obtain the 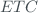 of the instrument to be calibrated where the subscript
of the instrument to be calibrated where the subscript 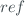 is associated to the reference instrument and the subscript
is associated to the reference instrument and the subscript 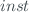 is related with the instrument to be calibrated.
is related with the instrument to be calibrated.
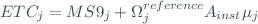
For a correctly characterized network instrument, the determined ETC values show a Gaussian distribution and the mean value is used as the instrument’s extra-terrestrial constant. One exception to this rule is the single monochromator Brewer models (MK-II and MK-IV) which are affected by stray light (Karppinen et al., 2015). In this case, the ETC distribution shows a tail at the lower ETC values for high Ozone Slant Column (OSC, the product of the total ozone content by the airmass). For this work we only the stray-light-free region is used to determine the ETC, which generally ranges from 300 to 800 DU in the OSC.
The network Brewers were calibrated using the one parameter ETC transfer method: i.e., the ozone differential absorption coefficient was derived from the calculations of wavelength calibration, the so-called “dispersion test” (Redondas et al., 2018c), applied to the spectroscopic set of the ozone cross section and, only the ozone ETC constant was transferred from the reference instrument.
The uncertainty of the ETC of the instrument can be obtained by the expanded uncertainty of equation ([eq:etc_cal]). Therefore, taking into account the synchronization time and the ozone variation with respect to the time difference of both instruments (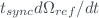 ), we can obtain the uncertainty
), we can obtain the uncertainty
![Equation $$\label{tran_unc}
u^{2}_{ETC} = \left[ A_{ins}\mu_{ins}\left( u_{\Omega_{ref}} + t_{sync}\frac{d\Omega_{ref}}{dt} \right) \right]^{2} + \left( \Omega_{ref}\mu_{ins}u_{A_{ins}}\right)^{2} + \left( \Omega_{ref}A_{ins}u_{\mu_{ins}} \right)^{2} + u^{2}_{MS9_{ins}}$$](/dokuwiki/lib/exe/fetch.php?media=wiki:latex:/img6669051cfc550f7a65a2191c669e5031.png)
The total uncertainty obtained for the ETC, transferring the calibration from the Brewer 185 to 183 is 2.51, in Dobson units (considering 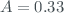 ,
, 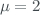 ). This value is mainly dominated for the statistical error (standard deviation) taking account a Type A evaluation (2.46 DU). Thus, the type B evaluation carried out through equation ([tran_unc]) just adds 0.5 DU in quadrature sum.
). This value is mainly dominated for the statistical error (standard deviation) taking account a Type A evaluation (2.46 DU). Thus, the type B evaluation carried out through equation ([tran_unc]) just adds 0.5 DU in quadrature sum.
Due to the presence of correlations that depend on the value of the ozone, on our error budget model the calculation of the components of each uncertainty with respect to the total makes it a non-trivial calculation. As a the first approximation we determine of the relative weights without correlations (Redondas and Cede, 2006). However, they will be included in future calculations to give a more accurate estimate of the contributions of each parameter to the total value.
The relative weights of the instrumental parameters determined during instrumental calibration have also been determined. Of all the parameters that affect the overall ozone uncertainty, the one corresponding to the ozone absorption coefficient covers approximately 85% of the total ozone uncertainty followed by the optical mass of the ozone layer with an average value of 6.5%. This last component becomes greater at high zenith angles and can reach 35% of the total value of the ozone uncertainty (Fig [fig:components]). Analyzing the sensitivity of the components of the optical mass of ozone, that is, the effective height of the ozone layer and the solar zenith angle, it can be seen how the SZA covers almost all of the uncertainty of the optical mass, being less important, in favor of the effective height, at high zenith angles (Fig. 1).
In the same way, the sensitivity study can be applied to the ozone absorption coefficient, in which more than 96% of this is covered by the uncertainty of the effective section of the ozone (Eq. [bicuad]). Most of these conclusions agree with the results presented by Redondas and Cede (2006).
The variables that are in second group regarding to the relative importance in the total uncertainty are the ETC and the measure (instrumental). The average relative weight of the ETC with respect to the total uncertainty stands at 4.5% for the reference instrument and 11.8% for the network instrument, while that of the measure is around 3.2% for both. As we have mentioned in Sec. 4, the type B uncertainty evaluation of the transfer uncertainty does not have very important role in the ETC transfer uncertainty. However, the source of error that contributes to the most of this uncertainty is the derivative of the ozone absorption component together with the error transferred from the reference instrument and the non-simultaneity of the data (see Figure 2). Only at high SZA, the optical mass component has a significant weight.
Because the instrumental parameters (i.e. dead time, temperature) and their uncertainties are cumulative and not expanded, it is not possible to do a sensitivity study, so the relative uncertainty of each correction with respect to this correction is estimated. In this way we see how (see Table [tab:instrumental]) how the temperature correction does not contribute a significant increase in the uncertainty of the measurement. On the other hand, once the double ratio of the measurements has been made, this uncertainty increases by more than a factor 2. The correction for the double ratio due to the non-linearity of the filters doubles the uncertainty of the measurement. Finally, we add that the most significant increase in the measurement uncertainty is due to the wavelength associated with dispersion. This increase can range from a factor of 3 to a factor of 4. With all this, the relative uncertainty of the measurement is around 0.26% regarding the measurement.
| Instrumental Correction | 183 | 185 |
|---|---|---|
| Raw-to-Count (320.1 nm) | 0.049 | 0.053 |
| Dark (320.1 nm) | 0.049 | 0.053 |
| Dead Time (320.1 nm) | 0.014 | 0.012 |
| Temperature (320.1 nm) | 0.014 | 0.013 |
| Double Ratio | 0.04 | 0.03 |
| Neutral Filters | 0.08 | 0.06 |
| Wavelength |  0.26 0.26 |  0.26 0.26 |
Table [tab:instrumental] shows the cumulative relative uncertainty of the instrumental parameters regarding instrumental corrections. As we see, the differences between brewer 183 and brewer 185 are negligible. There is a small decrease in the uncertainty from the dead time correction due to the change to logarithmic base.
In the case of measurement uncertainty, we see in Figure 3 that the differences are minimal. Obviously, not all spectrophotometers are the same and there will be small differences associated with temperature coefficients, filter linearity or dead time, among others. However, a sensitivity analysis of the sources of error such as the one presented with the standard ozone uncertainty is not possible since for each correction, the error is accumulated with the previous instrumental correction. Even so, we can see the relative uncertainty of the measurement with respect to the measurement (see Figure 3), and we can see the uncertainty of each instrumental correction with respect to the own correction (see Table [tab:instrumental]).
The Table [table_var] summarize all the variables used on the error analysis,they are classified on three main categories: Measurement, Model and Atmosphere with the values of two brewer algorithms, the standard algorithm and the Eubrewnet V2 algorithm. This V2 algorithm includes the Bremen ozone cross section and updated atmospheric model. This classification is not stray forward for some of the parameters by basically the measurement variables are the ones not affected by the algorithm. The paradigmatic case are Extraterrestrial constant, the concept is pure instrumental, is what the instrument measure outside of the atmosphere but is determined by Langley, regression to airmass zero, and the value depend of the atmosphere model.
| Component | Parameter | Standard Algorithm | V2 Algorithm | Comments |
|---|---|---|---|---|
raw counts counts | 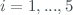 |
|||
| Cycles | ||||
| IT | sec | |||
| dark count | ||||
| dead time (dt) | sec | |||
U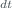 | (Fountoulakis et al., 2016) | |||
| Measurement | Temperature | 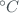 |
||
Temp. Coeff. (TC ) ) | 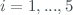 |
|||
U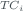 | 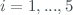 |
|||
MS9 Weights | 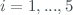 |
|||
| Filters (NF) | MS9 | |||
U | ||||
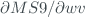 | MS9 | |||
U | ||||
| ETC | Langley, 1P transfer | |||
U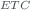 | Langley, 1P transfer | |||
O cross section cross section | BP | SG | (Bass and Paur, 1985), (Gorshelev et al., 2014) & (Serdyuchenko et al., 2013) | |
O absorption step absorption step | [5] | |||
| Model | dispersion file | |||
| Rayleigh coeff. (BE) | Bates | Nicolet | (Bates, 1984) & (Nicolet, 1984) | |
U | 1% | 0.5% | (Bates, 1984) & (Nicolet, 1984) | |
| A1 gradient | 9.36e-2% & 9.64e-3% | (Redondas et al., 2014a) | ||
| Pressure | climatology | barometer | ||
U | 15 mbar | 1.3 mbar | ||
T | -45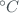 | -43.62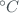 | ||
U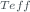 | 3.39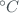 | 1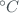 | ||
| Atmosphere | H | 22 km | 24.24 km | |
U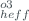 | 2.24 km | 0.5 km | ||
H | 5 km | 5 km | ||
U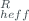 | 0.2 km | 0.25 km | ||
| time | ||||
| Ozone | ||||
| Ozone std | ||||
| Longitude | ||||
| Latitude | ||||
| Earth’s radio |
[table_var]
The measurement variables are mostly obtained from the database and the calibration reports of the instrument but they are some of the variables that are not reported and could require a reevaluation of the calibration or use a generic value when the reevaluation is not possible. These variables are:
The uncertainty of the ETC and the ozone of the reference instrument are also not usually reported on the calibration report of the network instruments.
The uncertainties of the due the atmospheric parameters used on this report are calculated for the conditions during IZO16 campaign, the influence of this parameters is the will be detailed on the next working package report.
The Eubrewnet database has been adapted and an access function provide the instrumental data necessary to obtain the uncertainty of the TOC through of Brewer spectrophotometers has been developed. (for example http:%%//%%eubrewnet.aemet.es/eubrewnet/data_test/uncert_input?brewerid=185&date=2016-09-21&format=text). The Python library which implement the error calculation is now on development.
Anon: EUBREWNET COST ES1207 website, [online] Available from: http://eubrewnet.aemet.es/cost1207 (Accessed October 2016a), n.d.
Anon: EUBREWNET data server, [online] Available from: http://eubrewnet.aemet.es/eubrewnet (Accessed June 2016b), n.d.
Bass, A. M. and Paur, R. J.: The ultraviolet cross-sections of ozone. I. The measurements. II - Results and temperature dependence, in Atmospheric ozone; proceedings of the quadrennial ozone symposium, halkidiki, greece, september 3-7, 1984 (a86-48601 24-46)., edited by C. S. Zerefos and A. Ghazi, pp. 606–616., 1985.
Bates, D. R.: Rayleigh scattering by air, Planetary and Space Science, 32(6), 785–790, 1984.
Berjón, A., Redondas, A., Sildoja, M.-M., Nevas, S., Wilson, K., León-Luis, S. F., El Gawhary, O. and Fountoulakis, I.: Sensitivity study of the instrumental temperature corrections on Brewer total ozone column measurements, Atmos. Meas. Tech., 11, 3323–3337, doi:10.5194/amt-2017-406, 2018.
Cuevas, E., Milford, C., Bustos, J. J., Campo-Hernández, R. del, García, O. E., García, R. D., Gómez-Peláez, A. J., Ramos, R., Redondas, A., Reyes, E., Rodriguez, S., Romero-Campos, P. M., Schneider, M., Belmonte, J., Gil-Ojeda, M., Almansa, F., Alonso-Pérez, S., Barreto, A., González-Morales, Y., Guirado-Fuentes, C., López-Solano, C., Afonso, S., Bayo, C., Berjón, A., Bethencourt, J., Camino, C., Carreño, V., Castro, N. J., Cruz, A. M., Damas, M., De Ory-Ajamil, F., García, M. I., Fernández-de Mesa, C. M., González, Y., Hernández, C., Hernández, Y., Hernández, M. A., Hernández-Cruz, B., Jover, M., Kühl, S. O., López-Fernández, R., López-Solano, J., Peris, A., Rodriguez-Franco, J. J., Sálamo, C., Sepúlveda, E. and Sierra, M.: Izaña Atmospheric Research Center Activity Report 2012-2014, State Meteorological Agency (AEMET), Madrid, Spain,; World Meteorological Organization, Geneva, Switzerland. [online] Available from: http://www.wmo.int/pages/prog/arep/gaw/documents/Final_GAW_Report_No_219.pdf (Accessed 30 June 2015), 2015.
Dobson, G. M. and Normand, C.: Determination of Constants Used in the Calculation of the Amount of Ozone from Spectrophotometer Measurements and the Accuracy of the Results, International Ozone Commission (I. A.M.A.P.), 1 [online] Available from: http://www.o3soft.eu/dobsonweb/messages/1957langleydobsonl.pdf, 1958.
El-Gawhary, O., Parra-Rojas, F. C. and Redondas, A.: Uncertainties in toc retrieval for brewer and dobson data and the role of cross-correlations among influence parameters, in ATMOZ workshop, el arenosillo, huelba. [online] Available from: https://repositorio.aemet.es/bitstream/20.500.11765/11736/1/Uncertainties_Gawhary.pdf, 2017.
Fountoulakis, I., Redondas, A., Bais, A. F., Rodriguez-Franco, J. J., Fragkos, K. and Cede, A.: Dead time effect on the Brewer measurements: Correction and estimated uncertainties, Atmos. Meas. Tech., 9(4), 1799–1816, doi:10.5194/amt-9-1799-2016, 2016.
Fountoulakis, I., Redondas, A., Bais, A. F., José Rodriguez-Franco, J., Fragkos, K. and Cede, A.: Dead time effect on the Brewer measurements: correction and estimated uncertainties, Atmospheric Measurement Techniques, 9(4), 1799–1816, doi:10.5194/amt-9-1799-2016, 2016.
Gorshelev, V., Serdyuchenko, A., Weber, M., Chehade, W. and Burrows, J. P.: High spectral resolution ozone absorption cross-sections - Part 1: Measurements, data analysis and comparison with previous measurements around 293 K, Atmospheric Measurement Techniques, 7(2), 609–624, doi:10.5194/amt-7-609-2014, 2014.
Gröbner, J., Wardle, D. I., McElroy, C. T. and Kerr, J. B.: Investigation of the wavelength accuracy of Brewer spectrophotometers, Appl. Opt., 37(36), 8352–8360, doi:10.1364/AO.37.008352, 1998.
Guides in Metrology, J. C. for: JCGM 100: Evaluation of measurement data - guide to the expression of uncertainty in measurement, JCGM., 2008.
Ito, M., Uesato, I., Noto, Y., Ijima, O., Shimizu, S., Takita, M., Shimodaira, H. and Ishitsuka, H.: Absolute Calibration for Brewer Spectrophotometers and Total Ozone/UV Radiation at Norikura on the Northern Japanese Alps, Journal of the Aerological Observatory, 72, 45–55, 2014.
Karppinen, T., Redondas, A., García, R. D., Lakkala, K., McElroy, C. T. and Kyrö, E.: Compensating for the Effects of Stray Light in Single-Monochromator Brewer Spectrophotometer Ozone Retrieval, Atmosphere-Ocean, 53(1), 66–73, doi:10.1080/07055900.2013.871499, 2015.
León-Luis, S. F., Redondas, A., Carreño, V., López-Solano, J., Berjón, A., Hernández-Cruz, B. and Santana-Díaz, D.: Internal consistency of the Regional Brewer Calibration Centre for Europe triad during the period 20052016, Atmospheric Measurement Techniques, 11(7), 4059–4072, doi:10.5194/amt-11-4059-2018, 2018.
Nicolet, M.: On the molecular scattering in the terrestrial atmosphere : An empirical formula for its calculation in the homosphere, Planetary and Space Science, 32(11), 1467–1468, doi:10.1016/0032-0633(84)90089-8, 1984.
Pujol, J.: The solution of nonlinear inverse problems and the Levenberg-Marquardt method, Geophysics, 72(4), W1–W16, doi:10.1190/1.2732552, 2007.
Redondas, A.: Izaña atmospheric observatory, ozone absolute calibration, Langley regression method., in The Eight Biennial WMO Consultation on Brewer Ozone and UV Spectrophotometer Operation, Calibration and Data Reporting., 2003.
Redondas, A. and Cede, A.: Brewer algorithm sensitivity analysis, in SAUNA workshop, puerto de la cruz, tenerife, vol. 286. [online] Available from: https://repositorio.aemet.es/bitstream/20.500.11765/6387/1/Brewer_Algorithm_Sensitiviy_Analysis.pdf, 2006.
Redondas, A., Evans, R., Stuebi, R., Köhler, U. and Weber, M.: Evaluation of the use of five laboratory-determined ozone absorption cross sections in Brewer and Dobson retrieval algorithms, Atmospheric Chemistry and Physics, 14(3), 1635–1648, doi:10.5194/acp-14-1635-2014, 2014a.
Redondas, A., Rodriguez, J., Carreno, V. and Sierra, M.: RBCC-E 2014 langley campaign the triad before Arosa/Davos campaing, [online] Available from: https://repositorio.aemet.es/bitstream/20.500.11765/2599/1/Alberto%20TriadArosaDavos.pdf, 2014b.
Redondas, A., Carreño, V., León-Luis, S. F., Hernández-Cruz, B., López-Solano, J., Rodriguez-Franco, J. J., Vilaplana, J. M., Gröbner, J., Rimmer, J., Bais, A. F., Savastiouk, V., Moreta, J. R., Boulkelia, L., Jepsen, N., Wilson, K. M., Shirotov, V. and Karppinen, T.: EUBREWNET RBCC-E Huelva 2015 Ozone Brewer Intercomparison, Atmospheric Chemistry and Physics, 18(13), 9441–9455, doi:10.5194/acp-18-9441-2018, 2018a.
Redondas, A., Carreño, V., Lui-León, S. F., Hernandez-Cruz, B., López-Solano, J., Rodríguez-Franco, J. J., Vilaplana, J. M., Gröbner, J., Rimmer, J., Bais, A. F. and al.: EUBREWNET rbcc-e huelva 2015 ozone brewer intercomparison – discussion, Atmos. Chem. Phys. Discuss., 2018, 1–18, doi:10.5194/acp-2017-1210, 2018b.
Redondas, A., Nevas, S., Berjón, A., Sildoja, M.-M., León-Luis, S. F., Carreño, V. and Santana-Díaz, D.: Wavelength calibration of Brewer spectrophotometer using a tunable pulsed laser and implications to the Brewer ozone retrieval, Atmospheric Measurement Techniques, 11(6), 3759–3768, doi:10.5194/amt-11-3759-2018, 2018c.
Serdyuchenko, A., Gorshelev, V., Weber, M., Chehade, W. and Burrows, J. P.: High spectral resolution ozone absorption cross-sections - Part 2: Temperature dependence, Atmospheric Measurement Techniques Discussions, 6, 6613–6643, doi:10.5194/amtd-6-6613-2013, 2013.
Weber, M., Gorshelev, V. and Serdyuchenko, A.: Uncertainty budgets of major ozone absorption cross sections used in UV remote sensing applications, Atmospheric Measurement Techniques, 9(9), 4459–4470, doi:https:%%//%%doi.org/10.5194/amt-9-4459-2016, 2016.
York, D.: Least-squares fitting of a straight line, Canadian Journal of Physics, 44, 1079, doi:10.1139/p66-090, 1966.
York, D.: Least squares fitting of a straight line with correlated errors, Earth and Planetary Science Letters, 5, 320–324, doi:10.1016/S0012-821X(68)80059-7, 1968.
We present the functions and data structure implemented in brewer_unc.py library. Other Python libraries to the Eubrewnet database can be found in the repository.
The functions of the brewer_unc.py module use two different data structures for both input and output. These structures are produced as the following Python dictionaries: measure and config which can be generated by brewerjson module.
This dictionary contains values extracted from DS Brewer measurements and O3L1 Brewer calculations. The dictionary also includes the station pressure uncertainty. Some of the dictionary field are used as input of the uncertainty calculations and other will be used as ouput. The values can be generated and downloaded through brewerjson module. The measure dictionary contains the following fields:
| Field | Description |
|---|---|
| ’gmt’ | datetime object |
| 'raw_count_w0 | raw counts wavelength #0 |
| 'raw_count_w1 | raw counts wavelength #1 |
| 'raw_count_w2 | raw counts wavelength #2 |
| 'raw_count_w3 | raw counts wavelength #3 |
| 'raw_count_w4 | raw counts wavelength #4 |
| 'raw_count_w5 | raw counts wavelength #5 |
| 'dark_count’ | dark count |
| ’cycles’ | # of cycles |
| ’temp’ | Brewer Temperature |
| ’nd_filter_position’ | ND filter position of #2 Filterwheel (in steps) |
| ’o3’ | Level 1 ozone |
| ’pre’ | pressure |
| ’u_pre’ | pressure uncertainty |
This dictionary contains the Brewer settings values. The values can came from B files, ICF files or Eubrewnet database through brewerjson. The config dictionary contains the following fields:
| Field | Description |
|---|---|
| ’w_o3_0’ | weight for double ratio #2 MS(9) calculation, for wavelength #0 |
| ’w_o3_2’ | weight for double ratio #2 MS(9) calculation, for wavelength #1 |
| ’w_o3_3’ | weight for double ratio #2 MS(9) calculation, for wavelength #2 |
| ’w_o3_4’ | weight for double ratio #2 MS(9) calculation, for wavelength #3 |
| ’w_o3_5’ | weight for double ratio #2 MS(9) calculation, for wavelength #4 |
| ’w_o3_6’ | weight for double ratio #2 MS(9) calculation, for wavelength #5 |
| ’o3tempcoef’ | ozone temperature coefficient for slit 0 |
| ’oslit1’ | ozone temperature coefficient for slit 1 |
| ’oslit2’ | ozone temperature coefficient for slit 2 |
| ’oslit3’ | ozone temperature coefficient for slit 3 |
| ’oslit4’ | ozone temperature coefficient for slit 4 |
| ’oslit5’ | ozone temperature coefficient for slit 5 |
| ’o3tempcoef_unc’ | ozone temperature coefficient uncertainty for slit 0 |
| ’oslit1_unc’ | ozone temperature coefficient uncertainty for slit 1 |
| ’oslit2_unc’ | ozone temperature coefficient uncertainty for slit 2 |
| ’oslit3_unc’ | ozone temperature coefficient uncertainty for slit 3 |
| ’oslit4_unc’ | ozone temperature coefficient uncertainty for slit 4 |
| ’oslit5_unc’ | ozone temperature coefficient uncertainty for slit 5 |
| 'it’ | slit sampling time |
| 'deadtime’ | dead time (seconds) |
| ’deadtime_unc’ | dead time uncertainty (seconds) |
| ’lf0’ | non-linearity filter coefficient of filter 0 |
| ’lf1’ | non-linearity filter coefficient of filter 1 |
| ’lf2’ | non-linearity filter coefficient of filter 2 |
| ’lf3’ | non-linearity filter coefficient of filter 3 |
| ’lf4’ | non-linearity filter coefficient of filter 4 |
| ’lf5’ | non-linearity filter coefficient of filter 5 |
| ’lf0_unc’ | non-linearity filter coefficient uncertainty of filter 0 |
| ’lf1_unc’ | non-linearity filter coefficient uncertainty of filter 1 |
| ’lf2_unc’ | non-linearity filter coefficient uncertainty of filter 2 |
| ’lf3_unc’ | non-linearity filter coefficient uncertainty of filter 3 |
| ’lf4_unc’ | non-linearity filter coefficient uncertainty of filter 4 |
| ’lf5_unc’ | non-linearity filter coefficient uncertainty of filter 5 |
| ’slope_wavelength’ | percent variation of double ratio with wavelength |
| ’slope_wavelength_unc’ | percent variation uncertainty of double ratio with wavelength |
| ’o3o3rate’ | ozone on ozone ratio |
| ’u_A1’ | ozone on ozone ratio uncertainty |
| ’latitude’ | site latitude in decimal degrees |
| ’longitude’ | site longitude in decimal degrees |
| ’be2’ | Rayleigh optical depth (multiplied by 10000*log10(e)) for wavelength #1 |
| ’be3’ | Rayleigh optical depth (multiplied by 10000*log10(e)) for wavelength #2 |
| ’be4’ | Rayleigh optical depth (multiplied by 10000*log10(e)) for wavelength #3 |
| ’be5’ | Rayleigh optical depth (multiplied by 10000*log10(e)) for wavelength #4 |
| ’be6’ | Rayleigh optical depth (multiplied by 10000*log10(e)) for wavelength #5 |
| ’etco3rate’ | ETC on ozone ratio |
| ’u_etc’ | ETC uncertainty on ozone ratio |
| ’rho_A_o3’ | Cross correlation coefficient between o3o3rate and o3 |
| ’rho_A_mu’ | Cross correlation coefficient between o3o3rate and ozone optical mass |
| ’rho_A_B’ | Cross correlation coefficient between o3o3rate and weighted Rayleigh depth |
| ’rho_A_m’ | Cross correlation coefficient between o3o3rate and Rayleigh optical mass |
| ’rho_A_p’ | Cross correlation coefficient between o3o3rate and pressure |
| ’rho_A_etc’ | Cross correlation coefficient between o3o3rate and ETC |
| ’rho_o3_mu’ | Cross correlation coefficient between o3 and ozone optical mass |
| ’rho_o3_B’ | Cross correlation coefficient between o3 and weighted Rayleigh depth |
| ’rho_o3_m’ | Cross correlation coefficient between o3 and Rayleigh optical mass |
| ’rho_o3_p’ | Cross correlation coefficient between o3 and pressure |
| ’rho_o3_etc’ | Cross correlation coefficient between o3 and ETC |
| ’rho_mu_B’ | Cross correlation coefficient between ozone optical mass and weighted Rayleigh depth |
| ’rho_mu_m’ | Cross correlation coefficient between ozone optical mass and Rayleigh optical mass |
| ’rho_mu_p’ | Cross correlation coefficient between ozone optical mass and pressure |
| ’rho_mu_etc’ | Cross correlation coefficient between ozone optical mass and ETC |
| ’rho_B_m’ | Cross correlation coefficient between weighted Rayleigh depth and Rayleigh optical mass |
| ’rho_B_p’ | Cross correlation coefficient between weighted Rayleigh depth and pressure |
| ’rho_B_etc’ | Cross correlation coefficient between weighted Rayleigh depth and ETC |
| ’rho_m_p’ | Cross correlation coefficient between Rayleigh optical mass and pressure |
| ’rho_m_etc’ | Cross correlation coefficient between Rayleigh optical mass and ETC |
| ’rho_p_etc’ | Cross correlation coefficient between pressure and ETC |
The functions of this module are separated in one principal section (Product functions) and in three auxiliary sections (airmass uncertainty, Data Reduction uncertainty and auxiliary functions).
| Function | Short Description |
|---|---|
| airmass_unc_calc() | Calculates the air mass uncertainty (rayleigh and ozone) for brewer individual measurements. |
| instrumental_unc() | Applies instrumental corrections (darkcount, deadtime, temperature, filter non-linearity) and variations (wavelength) uncertainties to brewer individual measurements. |
| combined() | Calculates the combined uncertainty to brewer individual measurements. |
This function calculates the air mass uncertainties for ozone and molecular atmosphere. To do this, it uses the functions solar_ha_dec_et_unc() and sza_unc()
Example
import datetime
import brewer_unc
measure = {u'gmt':datetime.datetime(2016, 9, 21, 12, 58, 42)}
config = {'latitude': 28.3081, 'longitude': 16.4992}
out=brewer_unc.airmass_unc_calc( measure, config )
print out['zenith_angle_uncertainty']
print out['airmass_uncertainty']
print out['airmass_rayleigh_uncertainty']
The field ’gmt’ is used from measure, and the fields ’latitude’ and ’longitude’ are used from config.
This function returns the input measure dictionary, adding the following fields:
* zenith_angle_uncertainty. This is calculated as the output of sza_unc() function.
* airmass_uncertainty. This is defined as the ozone air mass uncertainty, and is calculated as the output of brewer_airmass_unc(), using zenith_angle, zenith_angle_uncertainty, a height of 22 km and a height uncertainty of 2.24 km as input.
* airmass_rayleigh_uncertainty. This is defined as the Rayleigh air mass uncertainty, and is calculated as the output of brewer_airmass_unc(), using zenith_angle, zenith_angle_uncertainty, a height of 5 km and a height uncertainty of 0.2 km as input.
This function gets the uncertainties of raw counts to light intensity conversion (rawtocount()), in counts per seconds, as well as for instrument effects (dark count, dead time, temperature sensitivity and filter non-linearity). To do this, it uses the functions darkcount_unc(), deadtime_unc(), temp_unc() and filter_linearity_unc(). We can also obtain the MS9 variation uncertainty with the wavelength through the wavelength_slope() function.
Example
import datetime
import brewer_unc
measure = {u'raw_counts_w0': 254506,u'raw_counts_w1': 412550, u'raw_counts_w2': 612392, u'raw_counts_w3': 1328862,u'raw_counts_w4': 1757504,u'raw_counts_w5': 2109367,u'dark_count': 164,u'cycles': 20,u'temp': 24.0,u'nd_filter_position': 192}
config = {'w_o3_3': -1.0, 'oslit5': -0.11, 'it': 0.1147, 'oslit4': 0.02, 'w_o3_2': 0.0, 'w_o3_6': -1.7, 'w_o3_5': 2.2, 'w_o3_4': 0.5, 'oslit1': 0.0,'oslit3': -0.1, 'oslit2': -0.14, 'deadtime': 2.9e-08, 'w_o3_0': 0.0, 'deadtime_unc': 1e-9, 'o3tempcoef': 0.0, 'o3tempcoef_unc': 0.0, 'oslit1_unc': 0.0, 'oslit2_unc': 0.00025, 'oslit3_unc': 0.00058, 'oslit4_unc': 0.00071, 'oslit5_unc': 0.001,'lf0':0.0,'lf1':-2.3,'lf2':-5.27,'lf3':-19.32,'lf4':-27.36,'lf5':1.1,'lf0_unc': 0.0, 'lf1_unc': 1.74,'lf2_unc': 1.94,'lf3_unc': 1.75,'lf4_unc': 1.95,'lf5_unc': 4.31, 'slope_wavelength': 0.0518, 'slope_wavelength_unc': 0.25}
out = instrumental_unc( measure, config )
print("unc_measurement: "+str(out['measure_unc']))
The fields ’nd_filter_position’, ’cycles’, ’raw_counts_w0’, ’dark_count’, ’raw_counts_w1’, ’raw_counts_w2’, ’raw_counts_w3’, ’raw_counts_w4’, ’raw_counts_w5’ and ’temp’ are used from measure, and the fields ’deadtime’, ’deadtime_unc’, ’it’, ’o3tempcoef’, ’oslit1’, ’oslit2’, ’oslit3’, ’oslit4’, ’oslit’ ’o3tempcoef_unc’, ’oslit1_unc’, ’oslit2_unc’, ’oslit3_unc’, ’oslit4_unc’, ’oslit5_unc’, ’lf0’, ’lf1’, ’lf2’, ’lf3’,’lf4’,’lf5’, ’lf0_unc’, ’lf1_unc’, ’lf2_unc’, ’lf3_unc’, ’lf4_unc’,’lf5_unc’, ’w_o3_0’, ’w_o3_2’, ’w_o3_3’, ’w_o3_4’, ’w_o3_5’, ’w_o3_6’, ’slope_wavelength’ and ’slope_wavelength_unc’ are used from config.
This function returns the input measure dictionary, adding the following fields:
* ’nd_filter’. This field is calculated as the integer value of:
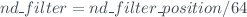
* ’single_ratio1’, ’single_ratio2’, ’single_ratio3’ and ’single_ratio4’. These fields are calculates as:
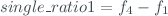

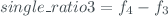
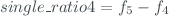
* ’double_ratio2’ and ’double_ratio2_unc’. These fields are calculated as:
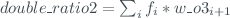

* 'measure' and 'measure\_unc'. These fields are obtained as:
![Math $measure = double\_ratio2 + LF[p]$](/dokuwiki/lib/exe/fetch.php?media=wiki:latex:/img3d141cf9760c4f352c6c65a5b14b6704.png)

This function obtains the correct value of the TOC uncertainty budget of the Brewer spectrophotometers through the function combined_uncertainty().
Example
import datetime
import brewer_unc
measure = {u'measure_unc': 6.97,u'airmass': 1.13,u'airmass_uncertainty': 0.00011,u'airmass_rayleigh': 1.13,u'airmass_rayleigh_uncertainty': 1.12e-5,u'o3': 280.67,u'pre': 770, u'u_pre': 15}
config = {'o3o3rate': 0.342,'B': 1.0, 'u_B': 0.029,'u_A1': 0.0094, 'u_etc': 9.14,'w_o3_2': 0.0, 'w_o3_6': -1.7, 'w_o3_5': 2.2, 'w_o3_4': 0.5,'w_o3_3': -1.0,'rho_A_o3': -0.0036, 'rho_A_mu': -0.97, 'rho_A_B': -0.17, 'rho_A_m': -0.15, 'rho_A_p': -0.000225, 'rho_A_etc': 0.0012, 'rho_o3_mu': -0.00036, 'rho_o3_B': -5.7e-05, 'rho_o3_m': -4.6e-05, 'rho_o3_p': -6.8e-08, 'rho_o3_etc': 4.2e-07, 'rho_mu_B': -0.011, 'rho_mu_m': -0.011, 'rho_mu_p': -9.11e-06, 'rho_mu_etc': 7.5e-05, 'rho_B_m': -0.0012, 'rho_B_p': -2e-06, 'rho_B_etc': 1.24e-05, 'rho_m_p': -2.08e-06, 'rho_m_etc': 1.3e-05, 'rho_p_etc': 1.9e-08}
out = combined( measure, config )
print("u_o3: " + str(out['u_o3']))
print("o3 : " +str(out['o3']))
The fields ’measure\_unc’, ’airmass’, ’airmass_uncertainty’, ’airmass_rayleigh’, ’airmass_rayleigh_uncertainty’, ’o3’, ’pre’ and ’u_pre’ are used from measure, and ’o3o3rate’, ’B’, ’u_B’, 'u_A1’, ’u_etc’, ’w_o3_0’, ’w_o3_2’, ’w_o3_3’, ’w_o3_4’, ’w_o3_5’, ’w_o3_6’,’rho_A_o3’, ’rho_A_mu’, ’rho_A_B’, ’rho_A_m’, ’rho_A_p’, ’rho_A_etc’, ’rho_o3_mu’, ’rho_o3_B’, ’rho_o3_m’, ’rho_o3_p’, ’rho_o3_etc’, ’rho_mu_B’, ’rho_mu_m’, ’rho_mu_p’, ’rho_mu_etc’, ’rho_B_m’, ’rho_B_p>’, ’rho_B_etc>’, ’rho_m_p’, ’rho_m_etc’, ’rho_p_etc’ are used from config.
This function returns the input measure dictionary, adding the following fields:
* ’u_o3’ which is calculated with the combined uncertainty equations.
| Function | Short Description |
|---|---|
| solar_ha_dec_et_unc() | Returns the solar hour angle, declination and equation of time uncertainties. |
| sza_unc() | Returns the solar zenith angle uncertainty. |
This function returns the solar hour angle, declination and equation of time uncertainties for a specific day at a specific location. In this case only geographic longitude is required to specify the location.
Example
brewer_unc.solar_ha_dec_et_unc( datet, lon )
The input parameter datet is a python datetime object. lon is a float that represents the geographic longitude in degrees.
The solar_ha_dec_et_unc() function returns a tuple with tree elements: the quadratic uncertainty of the hour angle in radians, quadratic uncertainty of the solar declination in radians and the quadratic uncertainty of the equation of time in minutes.
This function returns the solar zenith angle uncertainty for a specific day at a specific location.
Example
brewer_unc.sza_unc( datet, lat, lon )
The input parameter datet is a python datetime object. lat and lon are floats that represents the geographic latitude and longitude in degrees respectively.
The sza_unc() function returns a float with the value of the solar zenith angle uncertainty in degrees.
| Function | Short Description |
|---|---|
| rawtocount() | Returns a list with the raw-to-count conversion uncertainty. |
| darkcount_unc() | Returns a list with the dark count correction uncertainty. |
| deadtime_unc() | Returns a list with the dead time correction uncertainty. |
| temp_unc() | Returns a list with the temperature correction uncertainty. |
| filter_linearity_unc() | Returns a list with the filter linearity correction uncertainty. |
| wavelength_slope() | Returns a list with the uncertainty of the double ratio variation with wavelength. |
This function gets the uncertainty due to the conversion the raw-counts (counts per integration time) recorded by the spectrophotometer in count-rates (counts per second):
![Math $u_{out}^{2}[i] = \frac{2f[i]}{cycles*it}$](/dokuwiki/lib/exe/fetch.php?media=wiki:latex:/img36bfa572b4f8a73056172f455144563c.png)
Example
brewer_unc.rawtocount( raw, dark_raw, cycles, it )
The input parameter raw is a list of five integers with the raw measurements. dark_raw is a float with the raw dark value. cycles is an integer with the number of cycles for each measurement. it is a float with the slit sampling time.
The rawtocount() function returns a list with the uncertainty due to the conversion from raw-counts to count-rates, in counts per second.
This function gets the dark count correction uncertainty:
![Math $u_{out}^{2}[i] = u^{2}[i] + u^{2}[dark]$](/dokuwiki/lib/exe/fetch.php?media=wiki:latex:/img747a6f1f1a61616a31e7e61e8053ec30.png)
Example
brewer_unc.darkcount_unc( f, dark_count, u2_f, cycles, it )
The input parameter f is a list of five wavelength measurements. dark_count is a float with the dark count value. u2_f is a float with the quadratic uncertainty of the raw to count conversion. cycles is an integer with the number of cycles for each measurement. it is a float with the slit sampling time.
The darkcount_unc() function returns a list with the dark count corrected uncertainties in counts per second.
This function gets the dead time correction uncertainty. The method iterates 9 times the equation:
![Math $u_{out}^{2}[i] = \left(\frac{\exp(t1*f[i])}{1-t1*f[i]}\right)^{2}*u^{2}[i] + f^{4}[i]*u_{t1}^{2}$](/dokuwiki/lib/exe/fetch.php?media=wiki:latex:/img0e9a9070d4d15088dde7c7f356cc6821.png)
The deadtime-compensated uncertainty are normalized by computing the base ten logarithm of e, then scaled by 10000, thus allowing integer arithmetic.
![Math $u_{out} = \frac{10^{4}u[i]}{f[i]*\log(10)}$](/dokuwiki/lib/exe/fetch.php?media=wiki:latex:/img2688f5e9863d1ccbde807366dcdf97b1.png)
Example
brewer_unc.deadtime_unc( f, u2_f, t1, u_t1, norm=1 )
The input parameter f is a list of five floats with the measurements. u2_f is a list of five floats with the uncertainties. t1 is a float with the deadtime of the photon-counting system, u_t1 is a float with the dead time uncertainty of the photon-counting system.
The deadtime_unc() function returns a list with the dead time corrected uncertainty in counts per second.
This function gets the temperature-dependent compensation uncertainty of the spectrometer:
![Math $u_{out}^{2} = u^{2}[i] + tc^{2}[i]*u_{t}^{2} + t^{2}*u_{tc}^{2}[i]$](/dokuwiki/lib/exe/fetch.php?media=wiki:latex:/imgf7b3415af681dc7177a1b8c23b0f6ba4.png)
where 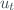 is the temperature uncertainty which usially is
is the temperature uncertainty which usially is 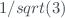 .
.
Example
brewer_unc.temp_unc( u2_f, t, tc, u_tc )
The input parameter u2_f is a list of five floats with the uncertainties. tc is list of five floats with the temperature coefficients. t is a float with the temperature of the system in Celsius degrees. u_tc is list of five floats with the temperature coefficient uncerainties.
The temp_unc() function returns a list with the temperature corrected uncertainties in counts per second.
This function gets the non-linearity of the neutral-density filters compensation uncertainty used to adjust the light level entering the spectrometer:
![Math $u_{out}^{2} = u^{2}[i] + u^{2}_{lf}[p]$](/dokuwiki/lib/exe/fetch.php?media=wiki:latex:/img1c55631ea3a427ac2cd0f08223e5602c.png)
This function is typically applied after the double ratio.
Example
brewer_unc.filter_linearity_unc( f, u_f, lf, u_lf, fp )
The input parameter f is a list of five floats with the measurements. u_f is a list of five floats with the uncertainties. lf is list of six floats with the non-linearity coefficient values of the neutral-density filters. u_lf is list of six floats with the non-linearity coefficient uncertainties of the neutral-density filters. fp is an integer with the filter position.
The filter_linearity_unc() function returns a list with the non-linearity corrected uncertainties.
This function gets the uncertainty of the double ratio variation with the wavelength:
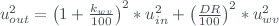
Example
brewer_unc.wavelength_slope( f, u_f, kwv, u_kwv )
The input parameter f is a list of floats with the double ratio. u_f is a list of floats with the double ratio uncertainties. kwv is a float with the double ratio variation coefficients with wavelength. u_kwv is a float with the double ratio variation coefficient uncertainties with wavelength.
The wavelength_slope() function returns a list with the double ratio variation with wavelength uncertainties.
| Function | Short Description |
|---|---|
| rel_unc() | Returns a list with the relative uncertainties. |
| wsum_unc() | Returns the weighted sum from all uncertainties on a list. |
| wsum() | Returns the weighted sum from all measurements on a list. |
| B_unc() | Returns the Rayleigh scattering uncertainty. |
This function computes the relative uncertainty of a list of measurements or parameters as following:
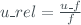
Example
import brewer_unc f=[1,2] u_f=[0.1,0.5] brewer_unc.rel_unc( f, u_f )
The input parameter f is a list of floats. u_f is list of of floats of the same length than f.
The rel_unc() function returns a float which is the relative uncertainty of f.
This function computes the sum of products over two lists. Both input lists should have the same length:
![Math $wsum = \sum_i f[i]*w[i]$](/dokuwiki/lib/exe/fetch.php?media=wiki:latex:/imgf65d50b3783f00a31f28c5e3f37bc7fe.png)
Example
import brewer f=[1,2] w=[2,3] brewer.wsum( f, w )
The input parameter f is a list of floats. w is list of of floats of the same length than f.
The wsum() function returns a float with the weighted sum value.
This function computes the sum of square products over two lists. Both input lists should have the same length:
![Math $wsum\_unc = \sum_i (f[i]*w[i])^2$](/dokuwiki/lib/exe/fetch.php?media=wiki:latex:/img2a2f6cc25b29cb34605b5e065bc565d1.png)
Example
import brewer f=[1,2] w=[0.1,0.5] brewer.wsum_unc( f, w )
The input parameter f is a list of floats. w is list of of floats of the same length than f.
The wsum() function returns a float with the weighted square sum value.
This function computes the uncertainty of the Rayleigh scattering coefficients.
Example
import brewer
config = {'w_o3_3': -1.0,'w_o3_2': 0.0, 'w_o3_6': -1.7, 'w_o3_5': 2.2, 'w_o3_4': 0.5,'be3': 4620, 'be6': 4040, 'be4': 4410, 'be5': 4220, 'be2': 4870 }
unc = 0.01
out = brewer.wsum_unc( config, unc )
print("u_B: " + str(out['u_B']))
print("B : " + str(out['B']))
The fields ’be2’, ’be3’, ’be4', ’be5’, ’be6’, ’w_o3_2’, ’w_o3_3’, ’w_o3_4’, ’w_o3_5’, ’w_o3_6’ and ’w_o3_0’ are used from config.
This function returns the input config dictionary, adding the following fields:
* ’B’. This field is the weighted Rayleigh scattering coefficient.
* ’u_B’. This field is the weighted Rayleigh scattering coefficient uncertainty.