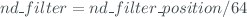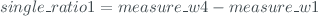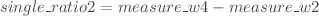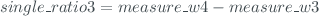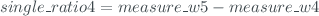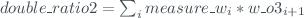Table of Contents
Brewer Python Library
We describe here the functions and data structured implemented in brewer.py library. A Python library to the Eubrewnet database can be found in the brewerjson module . The last version of the brewer python library is available from rbcce subversion repository.
Installation
Brewer library can be imported from python code adding the path to brewer.py module to the Python path (list of directories Python goes through to search for modules and files):
import sys
sys.path.append("/home/to/module/")
By default the sys.path variable includes the current directory, so if brewer.py is in the same directory as the Python script, the module can be directly imported.
Alternatively, you can download brewer.py file to the standard location for third-party Python modules. This location varies by platform and by how you built/installed Python itself. Typical locations are shown in the following table:
| Platform | Standard installation location |
|---|---|
| Windows | C:\PythonXY\Lib\site-packages |
| Unix | /usr/local/lib/pythonX.Y/site-packages |
Data structures
Functions from brewer.py module use four different data structures for both input and output. These structures are python dictionaries: measure, uv, hg, config and bdaily. These structures can be generated by using brewerjson module.
measure
Dictionary containing values of the DS and SL Brewer measurements. Some of the dictionary fields will be used as input to the calculations of the library functions, and others will be used as the output. The values can came from B files or from Eubrewnet database through its JSON interface by using brewerjson module. It contains the following fields:
| Field | Description |
|---|---|
| 'gmt' | datetime object |
| 'nd_filter_position' | ND filter position of #2 Filterwheel (in steps) |
| 'nd_filter' | ND filter position of #2 Filterwheel (index from 0 to 6) |
| 'cycles' | # of cycles |
| 'raw_counts_w0' | raw counts wavelength #0 |
| 'dark_count' | dark count |
| 'raw_counts_w0' | raw counts wavelength #0 |
| 'raw_counts_w1' | raw counts wavelength #1 |
| 'raw_counts_w2' | raw counts wavelength #2 |
| 'raw_counts_w3' | raw counts wavelength #3 |
| 'raw_counts_w4' | raw counts wavelength #4 |
| 'raw_counts_w5' | raw counts wavelength #5 |
| 'temp' | Brewer temperature |
| 'single_ratio1' | single ratio #1 MS(4) |
| 'single_ratio2' | single ratio #2 MS(5) |
| 'single_ratio3' | single ratio #3 MS(6) |
| 'single_ratio4' | single ratio #4 MS(7) |
| 'double_ratio1' | double ratio #1 MS(8) |
| 'double_ratio2' | double ratio #2 MS(9) |
| 'zenith_angle' | solar zenith angle |
| 'apparent_zenith_angle' | solar zenith angle corrected by atmospheric refraction |
| 'azimuth_angle' | solar azimuth angle |
| 'airmass' | air mass for ozone layer |
| 'airmass_rayleigh' | air mass for molecular atmosphere |
| 'measure_w0' | counts per second for wavelength #0 corrected by instrument effects |
| 'measure_w1' | counts per second for wavelength #1 corrected by instrument effects |
| 'measure_w2' | counts per second for wavelength #2 corrected by instrument effects |
| 'measure_w3' | counts per second for wavelength #3 corrected by instrument effects |
| 'measure_w4' | counts per second for wavelength #4 corrected by instrument effects |
| 'measure_w5' | counts per second for wavelength #5 corrected by instrument effects |
| 'o3' | ozone |
| 'so2' | sulphur dioxide |
| 'o3_sl' | ozone corrected by SL |
| 'so2_sl' | sulphur dioxide corrected by SL |
| 'o3_slcor' | SL correction for ozone |
| 'so2_slcor' | SL correction for sulphur dioxide |
| 'hg_flag' | Flag from HG measurement |
| 'n_summary' | Summary identifier to which the measure belongs |
uv
Dictionary containing values of the UV Brewer measurements, including uv, ux, and ua. Some of the dictionary fields will be used as input to the calculations of the library functions, and others will be used as the output. The values can came from B files or from Eubrewnet database through its JSON interface by using brewerjson module. It contains the following fields:
| Field | Description |
|---|---|
| 'brewerid' | Brewer ID number |
| 'scan' | UV scan type |
| 'it' | slit sampling time |
| 'deadtime' | Dead time (seconds) |
| 'cycles' | # of cycles |
| 'gmt' | datetime object |
| 'mmmm' | Time (GMT) in minutes for 1st wavelength |
| 'location' | Site Location |
| 'latitude' | Site latitude in decimal degrees (positive latitudes are north of the equator) |
| 'longitude' | Site longitude in decimal degrees (positive longitudes are west of the Prime Meridian) |
| 'temp' | Brewer temperature in volts |
| 'press' | Pressure |
| 'dark_count' | dark count |
| 'time' | list of datetime objects for each measurement |
| 'wavelengths' | list of wavelengths |
| 'steps' | list of micrometer steps |
| 'counts' | list of raw counts |
| 'irradiance' | list of irradiance values in W/m²/nm |
| 'duv' | Diffey-weighted UV irradiance in mW/m² |
| 'resdate' | Date of responsivity calibration used to calculate irradiance |
| 'straylight' | Stray light used to calculate irradiance |
uvr
Dictionary containing values of Brewer responsivity for de UV measurements, determined using a calibrated light source. It contains the following fields:
| Field | Description |
|---|---|
| 'brewerid' | Brewer ID number |
| 'date' | date of calibration |
| 'wavelengths' | list of wavelengths |
| 'responsivity' | list of responsivity values (counts/s)/(mW/m²/A) |
hg
Dictionary containing values of HG Brewer calibration. The values can came from B files or from Eubrewnet database through its JSON interface by using brewerjson module. It contains the following fields:
| Field | Description |
|---|---|
| 'gmt' | datetime object |
| 'step2' | Micrometer set to this step # |
config
Dictionary containing values of brewer settings. The values can came from B files, from ICF or from Eubrewnet database through its JSON interface by using brewerjson module. It contains the following fields:
| Field | Description |
|---|---|
| 'latitude' | Site latitude in decimal degrees (positive latitudes are north of the equator) |
| 'longitude' | Site longitude in decimal degrees (positive longitudes are west of the Prime Meridian) |
| 'press' | Pressure |
| 'o3tempcoef' | Ozone temperature coefficient for slit 0 |
| 'oslit1' | Ozone temperature coefficient for slit 1 |
| 'oslit2' | Ozone temperature coefficient for slit 2 |
| 'oslit3' | Ozone temperature coefficient for slit 3 |
| 'oslit4' | Ozone temperature coefficient for slit 4 |
| 'oslit5' | Ozone temperature coefficient for slit 5 |
| 'o3o3rate' | Ozone on ozone ratio |
| 'so2so2rate' | SO 2 on SO 2 ratio |
| 'o3so2rate' | Ozone on SO 2 ratio |
| 'etco3rate' | ETC on ozone ratio |
| 'etcso2rate' | ETC on SO 2 ratio |
| 'deadtime' | Dead time (seconds) |
| 'nfilter0' | Neutral density of filter 0 |
| 'nfilter1' | Neutral density of filter 1 |
| 'nfilter2' | Neutral density of filter 2 |
| 'nfilter3' | Neutral density of filter 3 |
| 'nfilter4' | Neutral density of filter 4 |
| 'nfilter5' | Neutral density of filter 5 |
| 'it' | slit sampling time |
| 'be2' | Rayleigh optical depth ( multiplied by 10000*log10(e) ) for wavelength #1 |
| 'be3' | Rayleigh optical depth ( multiplied by 10000*log10(e) ) for wavelength #2 |
| 'be4' | Rayleigh optical depth ( multiplied by 10000*log10(e) ) for wavelength #3 |
| 'be5' | Rayleigh optical depth ( multiplied by 10000*log10(e) ) for wavelength #4 |
| 'be6' | Rayleigh optical depth ( multiplied by 10000*log10(e) ) for wavelength #5 |
| 'w_so2_0' | weight for double ratio #1 MS(8) calculation, for wavelength #0 |
| 'w_so2_2' | weight for double ratio #1 MS(8) calculation, for wavelength #1 |
| 'w_so2_3' | weight for double ratio #1 MS(8) calculation, for wavelength #2 |
| 'w_so2_4' | weight for double ratio #1 MS(8) calculation, for wavelength #3 |
| 'w_so2_5' | weight for double ratio #1 MS(8) calculation, for wavelength #4 |
| 'w_so2_6' | weight for double ratio #1 MS(8) calculation, for wavelength #5 |
| 'w_o3_0' | weight for double ratio #2 MS(9) calculation, for wavelength #0 |
| 'w_o3_2' | weight for double ratio #2 MS(9) calculation, for wavelength #1 |
| 'w_o3_3' | weight for double ratio #2 MS(9) calculation, for wavelength #2 |
| 'w_o3_4' | weight for double ratio #2 MS(9) calculation, for wavelength #3 |
| 'w_o3_5' | weight for double ratio #2 MS(9) calculation, for wavelength #4 |
| 'w_o3_6' | weight for double ratio #2 MS(9) calculation, for wavelength #5 |
| 'sl_r5' | Calibration reference for double ratio #1 of standard lamp |
| 'sl_r6' | Calibration reference for double ratio #2 of standard lamp |
| 'wstepn' | Micrometer set on installation to this step # |
bdaily
Dictionary containing daily values calculated from the individual SL measurements. It contains the following fields:
| Field | Description |
|---|---|
| 'date' | Date object |
| 'sl_r5_median' | R5 daily median of individual SL measurements |
| 'sl_r6_median' | R6 daily median of individual SL measurements |
| 'sl_num' | Number of measures used to calculate the daily median |
| 'sl_r5_tma' | Triangular movil average of R5 daily median |
| 'sl_r6_tma' | Triangular movil average of R6 daily median |
| 'sl_num_tma' | Number of measures used to calculate the Triangular movil average |
Functions
The functions of this module are separated into two main sections (Products and Control functions) and four auxiliary sections (Astronomical, Airmass, Data Reduction, and Auxiliary functions).
Products
| Function | Short Description |
|---|---|
| airmass_calc() | Calculates sun position and air mass (rayleigh and ozone) for brewer individual measurements. |
| airmass_calcl() | Calculates sun position and air mass (rayleigh and ozone) for a list of brewer measurements. |
| instrumental_cor() | Applies instrumental corrections (darkcount, deadtime, temperature, filter attenuation) to brewer individual measurements. |
| instrumental_corl() | Applies instrumental corrections (darkcount, deadtime, temperature, filter attenuation) to a list of brewer measurements. |
| rayleigh_cor() | Applies Rayleigh corrections to brewer instrumentally corrected individual measurements. |
| rayleigh_corl() | Applies Rayleigh corrections to a list of brewer instrumentally corrected measurements. |
| o3_so2() | Calculates 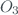 and and  from the brewer corrected individual measurements. from the brewer corrected individual measurements. |
| o3_so2_sl() | Calculates Standard Lamp correction for 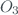 and and  . . |
| uv_cal() | Calculates UV Irradiance and DUV. |
airmass_calc()
This function calculates sun position and air masses for ozone and molecular atmosphere. To do this, it uses the functions solar_zenith_angle(), solar_azimuth_angle(), brewer_airmass() and apparent_zenith_angle().
Example
import datetime
import brewer
measure={u'raw_counts_w4': 856609, u'raw_counts_w5': 880063, u'raw_counts_w0': 474, u'raw_counts_w1': 49601, u'raw_counts_w2': 172448, u'raw_counts_w3': 530003, u'airmass': 2.144, u'nd_filter_position': 64, u'mmmm_gmt': 901.63, u'dark_count': 126, u'hg_flag': -1, u'gmt': datetime.datetime(2009, 6, 3, 15, 1, 37), u'double_ratio1': 12021, u'double_ratio2': 5834, u'upper_slit': 6, u'n_summary': 107, u'mmmm': 1010.21452648741, u'date': u'20090603', u'single_ratio4': -291, u'single_ratio1': 11097, u'single_ratio3': 1720, u'single_ratio2': 6196, u'lower_slit': 0, u'temp': 21.0, u'zenith_angle': 62.559, u'filter': 97, u'cycles': 20}
config={'w_so2_4': 0.0, 'w_so2_5': 4.2, 'w_so2_6': -3.2, 'w_o3_3': -1.0, 'w_so2_2': -1.0, 'w_so2_3': 0.0, 'oslit5': 5.3703, 'it': 0.1147, 'oslit4': 6.738, 'date': datetime.date(2009, 6, 3), 'nfilter2': 10000, 'etcso2rate': 2980.0, 'sl_r6': 1875.0, 'sl_r5': 3405.0, 'latitude': 67.3675, 'be3': 4620, 'be6': 4040, 'be4': 4410, 'be5': 4220, 'be2': 4870, 'press': 990.0, 'w_o3_2': 0.0, 'so2so2rate': 2.35, 'w_o3_6': -1.7, 'w_o3_5': 2.2, 'w_o3_4': 0.5, 'o3so2rate': 1.13903, 'etco3rate': 3101.0, 'oslit1': 7.42, 'nfilter5': 25000, 'oslit3': 7.0417, 'oslit2': 7.2467, 'nfilter0': 0, 'nfilter1': 5000, 'longitude': -26.633, 'nfilter3': 15000, 'nfilter4': 20000, 'o3o3rate': 0.3449, 'deadtime': 3.5e-08}
out=brewer.airmass_calc(measure,config)
print out['zenith_angle']
print out['apparent_zenith_angle']
print out['azimuth_angle']
print out['airmass']
print out['airmass_rayleigh']
The field 'gmt' is used from measure, and the fields 'latitude' and 'longitude' are used from config.
This function returns the input measure dictionary, adding the following fields:
- 'zenith_angle'. This is calculated as the output of solar_zenith_angle() function.
- 'azimuth_angle'. This is calculated as the output of solar_azimuth_angle() function.
- 'apparent_zenith_angle'. This is calculated as the output of apparent_zenith_angle() function, using 'zenith_angle' as input.
- 'airmass'. This is defined as the ozone air mass, and is calculated as the output of brewer_airmass(), using 'zenith_angle' and a height of 22km as input.
- 'airmass_rayleigh'. This is defined as the Rayleigh air mass, and is calculated as the output of brewer_airmass(), using 'zenith_angle' and a height of 5km as input.
airmass_calcl()
This function applies airmass_calc() to a list of brewer measuremments. It accepts two input parameters: 'measure' and 'config'.
- 'measure' is a list of measurements ds, sl, etc.
- 'config' is a list of dictionaries with brewer configurations.
Example
import datetime import brewer import brewerjson brewerid=185 user='user' password='password' date1=datetime.date(2012,2,7) date2=datetime.date(2012,2,8) ds=brewerjson.getDataList(brewerid,user,password,"DS",date1,date2) config=brewerjson.getDataList(brewerid,user,password,"ConfigbyDate",date1,date2) ds=brewer.airmass_calcl(ds,config)
instrumental_cor()
This function converts raw counts to light intensity, in counts per seconds, while correcting for instrument effects (dark count, dead time, temperature sensitivity and filter attenuation). To do this, it uses the functions darkcount_cor(), deadtime_cor(), temp_cor() and attenuation_cor().
Example
import datetime
import brewer
measure={u'raw_counts_w4': 856609, u'raw_counts_w5': 880063, u'raw_counts_w0': 474, u'raw_counts_w1': 49601, u'raw_counts_w2': 172448, u'raw_counts_w3': 530003, u'airmass': 2.144, u'nd_filter_position': 64, u'mmmm_gmt': 901.63, u'dark_count': 126, u'hg_flag': -1, u'gmt': datetime.datetime(2009, 6, 3, 15, 1, 37), u'double_ratio1': 12021, u'double_ratio2': 5834, u'upper_slit': 6, u'n_summary': 107, u'mmmm': 1010.21452648741, u'date': u'20090603', u'single_ratio4': -291, u'single_ratio1': 11097, u'single_ratio3': 1720, u'single_ratio2': 6196, u'lower_slit': 0, u'temp': 21.0, u'zenith_angle': 62.559, u'filter': 97, u'cycles': 20}
config={'w_so2_4': 0.0, 'w_so2_5': 4.2, 'w_so2_6': -3.2, 'w_o3_3': -1.0, 'w_so2_2': -1.0, 'w_so2_3': 0.0, 'oslit5': 5.3703, 'it': 0.1147, 'oslit4': 6.738, 'date': datetime.date(2009, 6, 3), 'nfilter2': 10000, 'etcso2rate': 2980.0, 'sl_r6': 1875.0, 'sl_r5': 3405.0, 'latitude': 67.3675, 'be3': 4620, 'be6': 4040, 'be4': 4410, 'be5': 4220, 'be2': 4870, 'press': 990.0, 'w_o3_2': 0.0, 'so2so2rate': 2.35, 'w_o3_6': -1.7, 'w_o3_5': 2.2, 'w_o3_4': 0.5, 'o3so2rate': 1.13903, 'etco3rate': 3101.0, 'oslit1': 7.42, 'nfilter5': 25000, 'oslit3': 7.0417, 'oslit2': 7.2467, 'nfilter0': 0, 'nfilter1': 5000, 'longitude': -26.633, 'nfilter3': 15000, 'nfilter4': 20000, 'o3o3rate': 0.3449, 'deadtime': 3.5e-08}
out=brewer.instrumental_cor(measure,config)
print out['double_ratio1']
print out['double_ratio2']
The fields 'nd_filter_position', 'cycles', 'raw_counts_w0', 'dark_count', 'raw_counts_w1', 'raw_counts_w2', 'raw_counts_w3', 'raw_counts_w4', 'raw_counts_w5' and 'temp' are used from measure, and the fields 'deadtime', 'it', 'nfilter0', 'nfilter1', 'nfilter2', 'nfilter3', 'nfilter4', 'nfilter5', 'oslit1', 'oslit2', 'oslit3', 'oslit4', 'oslit5', 'w_o3_2', 'w_o3_3', 'w_o3_4', 'w_o3_5', 'w_o3_6', 'w_so2_2', 'w_so2_3', 'w_so2_4', 'w_so2_5' and 'w_so2_6' are used from config.
This function returns the input measure dictionary, adding the following fields:
- 'measure_w1', 'measure_w2', 'measure_w3', 'measure_w4' and 'measure_w5'. These fields are the output of the consecutive application of darkcount_cor(), deadtime_cor(), temp_cor() and attenuation_cor() functions.
- 'nd_filter'. This field is calculated as the integer value of:
- 'single_ratio1', 'single_ratio2', 'single_ratio3' and 'single_ratio4'. These fields are calculates as:
- 'double_ratio1' and 'double_ratio2'. These fields are calculated as:
instrumental_corl()
This function applies instrumental_cor() to a list of brewer measuremments. It accepts two input parameters: 'measure' and 'config'.
- 'measure' is a list of measurements ds, sl, etc.
- 'config' is a list of dictionaries with brewer configurations.
Example
import datetime import brewer import brewerjson brewerid=185 user='user' password='password' date1=datetime.date(2012,2,7) date2=datetime.date(2012,2,8) sl=brewerjson.getDataList(brewerid,user,password,"SL",date1,date2) config=brewerjson.getDataList(brewerid,user,password,"ConfigbyDate",date1,date2) sl=brewer.instrumental_corl(sl,config)
rayleigh_cor()
This function compensates the absorption of the molecular atmosphere to each channel signal, taking into account the atmospheric pressure:
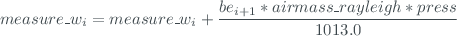
where 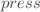 is the mean Barometric Pressure of the Site in mBar and
is the mean Barometric Pressure of the Site in mBar and 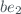 ,
, 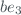 ,
,  ,
, 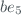 and
and 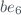 are the scaled Rayleigh optical depth:
are the scaled Rayleigh optical depth:
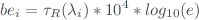
Once 'measure_w1', 'measure_w2', 'measure_w3', 'measure_w4' and 'measure_w5' fileds are updated, singe and double ratios are also updated.
Example
import datetime
import brewer
measure={u'raw_counts_w4': 856609, u'raw_counts_w5': 880063, u'raw_counts_w0': 474, u'raw_counts_w1': 49601, u'raw_counts_w2': 172448, u'raw_counts_w3': 530003, u'airmass': 2.144, u'nd_filter_position': 64, u'mmmm_gmt': 901.63, u'dark_count': 126, u'hg_flag': -1, u'gmt': datetime.datetime(2009, 6, 3, 15, 1, 37), u'double_ratio1': 12021, u'double_ratio2': 5834, u'upper_slit': 6, u'n_summary': 107, u'mmmm': 1010.21452648741, u'date': u'20090603', u'single_ratio4': -291, u'single_ratio1': 11097, u'single_ratio3': 1720, u'single_ratio2': 6196, u'lower_slit': 0, u'temp': 21.0, u'zenith_angle': 62.559, u'filter': 97, u'cycles': 20}
config={'w_so2_4': 0.0, 'w_so2_5': 4.2, 'w_so2_6': -3.2, 'w_o3_3': -1.0, 'w_so2_2': -1.0, 'w_so2_3': 0.0, 'oslit5': 5.3703, 'it': 0.1147, 'oslit4': 6.738, 'date': datetime.date(2009, 6, 3), 'nfilter2': 10000, 'etcso2rate': 2980.0, 'sl_r6': 1875.0, 'sl_r5': 3405.0, 'latitude': 67.3675, 'be3': 4620, 'be6': 4040, 'be4': 4410, 'be5': 4220, 'be2': 4870, 'press': 990.0, 'w_o3_2': 0.0, 'so2so2rate': 2.35, 'w_o3_6': -1.7, 'w_o3_5': 2.2, 'w_o3_4': 0.5, 'o3so2rate': 1.13903, 'etco3rate': 3101.0, 'oslit1': 7.42, 'nfilter5': 25000, 'oslit3': 7.0417, 'oslit2': 7.2467, 'nfilter0': 0, 'nfilter1': 5000, 'longitude': -26.633, 'nfilter3': 15000, 'nfilter4': 20000, 'o3o3rate': 0.3449, 'deadtime': 3.5e-08}
out=brewer.airmass_calc(measure,config)
out=brewer.instrumental_cor(out,config)
out=brewer.rayleigh_cor(out,config)
print out['double_ratio1']
print out['double_ratio2']
The fields 'measure_w1', 'measure_w2', 'measure_w3', 'measure_w4', 'measure_w5' and 'airmass_rayleigh' are used from measure, and the fields 'press', 'be2', 'be3', 'be4', 'be5', 'be6', 'w_o3_2', 'w_o3_3', 'w_o3_4', 'w_o3_5', 'w_o3_6', 'w_so2_2', 'w_so2_3', 'w_so2_4', 'w_so2_5' and 'w_so2_6' are used from config.
This function returns the input measure dictionary, updating the following fields as described above: 'measure_w1', 'measure_w2', 'measure_w3', 'measure_w4', 'measure_w5', 'single_ratio1', 'single_ratio2', 'single_ratio3', 'single_ratio4', 'double_ratio1' and 'double_ratio2'.
rayleigh_corl()
This function applies rayleigh_corl() to a list of brewer instrumentally corrected measurements. It accepts two input parameters: 'measure' and 'config'.
- 'measure' is a list of measurements ds, sl, etc.
- 'config' is a list of dictionaries with brewer configurations.
Example
import datetime import brewer import brewerjson brewerid=185 user='user' password='password' date1=datetime.date(2012,2,7) date2=datetime.date(2012,2,8) ds=brewerjson.getDataList(brewerid,user,password,"DS",date1,date2) config=brewerjson.getDataList(brewerid,user,password,"ConfigbyDate",date1,date2) ds=brewer.airmass_calcl(ds,config) ds=brewer.instrumental_corl(ds,config) ds=brewer.rayleigh_corl(ds,config)
o3_so2()
This function computes 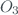 and
and  amount from Brewer measurements:
amount from Brewer measurements:

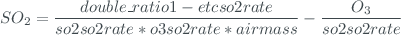
Example
import datetime
import brewer
measure={u'raw_counts_w4': 856609, u'raw_counts_w5': 880063, u'raw_counts_w0': 474, u'raw_counts_w1': 49601, u'raw_counts_w2': 172448, u'raw_counts_w3': 530003, u'airmass': 2.144, u'nd_filter_position': 64, u'mmmm_gmt': 901.63, u'dark_count': 126, u'hg_flag': -1, u'gmt': datetime.datetime(2009, 6, 3, 15, 1, 37), u'double_ratio1': 12021, u'double_ratio2': 5834, u'upper_slit': 6, u'n_summary': 107, u'mmmm': 1010.21452648741, u'date': u'20090603', u'single_ratio4': -291, u'single_ratio1': 11097, u'single_ratio3': 1720, u'single_ratio2': 6196, u'lower_slit': 0, u'temp': 21.0, u'zenith_angle': 62.559, u'filter': 97, u'cycles': 20}
config={'w_so2_4': 0.0, 'w_so2_5': 4.2, 'w_so2_6': -3.2, 'w_o3_3': -1.0, 'w_so2_2': -1.0, 'w_so2_3': 0.0, 'oslit5': 5.3703, 'it': 0.1147, 'oslit4': 6.738, 'date': datetime.date(2009, 6, 3), 'nfilter2': 10000, 'etcso2rate': 2980.0, 'sl_r6': 1875.0, 'sl_r5': 3405.0, 'latitude': 67.3675, 'be3': 4620, 'be6': 4040, 'be4': 4410, 'be5': 4220, 'be2': 4870, 'press': 990.0, 'w_o3_2': 0.0, 'so2so2rate': 2.35, 'w_o3_6': -1.7, 'w_o3_5': 2.2, 'w_o3_4': 0.5, 'o3so2rate': 1.13903, 'etco3rate': 3101.0, 'oslit1': 7.42, 'nfilter5': 25000, 'oslit3': 7.0417, 'oslit2': 7.2467, 'nfilter0': 0, 'nfilter1': 5000, 'longitude': -26.633, 'nfilter3': 15000, 'nfilter4': 20000, 'o3o3rate': 0.3449, 'deadtime': 3.5e-08}
out=brewer.airmass_calc(measure,config)
out=brewer.instrumental_cor(out,config)
out=brewer.rayleigh_cor(out,config)
out=brewer.o3_so2(out,config)
print out['o3']
print out['so2']
The fields 'double_ratio1', 'double_ratio2' and 'airmass' are used from measure, and the fields 'etco3rate', 'etcso2rate', 'o3o3rate', 'so2so2rate' and 'o3so2rate' are used from config.
This function returns the input measure structure, adding the following fields, calculated as described above: 'o3' and 'so2'
o3_so2_sl()
This function computes the standard lamp correction for 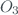 and
and  . It is calculated as the normalized difference between the averaged value of double ratio value from SL measurements and the double ratio value stored during calibration.
. It is calculated as the normalized difference between the averaged value of double ratio value from SL measurements and the double ratio value stored during calibration.
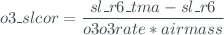
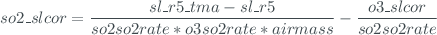
![Equation \begin{displaymath}
\[ o3\_sl =
\begin{cases}
o3 & \quad \text{if } abs(sl\_r6\_tma - sl\_r6) < mindu\\
o3 + o3\_slcor & \quad \text{if } abs(sl\_r6\_tma - sl\_r6) \geq mindu\\
\end{cases}
\]
\end{displaymath}](/dokuwiki/lib/exe/fetch.php?media=wiki:latex:/img55c59bbb2a4ad0b305c853ca34c43a5b.png)
![Equation \begin{displaymath}
\[ so2\_sl =
\begin{cases}
so2 & \quad \text{if } abs(sl\_r6\_tma - sl\_r6) < mindu\\
so2 + so2\_slcor & \quad \text{if } abs(sl\_r6\_tma - sl\_r6) \geq mindu\\
\end{cases}
\]
\end{displaymath}](/dokuwiki/lib/exe/fetch.php?media=wiki:latex:/img94de77b3e9dea6e0c766c9a32edb37d3.png)
Example
brewer.o3_so2_sl(measure,config,bdaily,mindu=5)
The fields 'o3', 'so2' and 'airmass' are used from measure, the fields 'o3o3rate', 'so2so2rate', 'o3so2rate', 'sl_r5' and 'sl_r6' are used from config, and the fields 'sl_r5_tma' and 'sl_r6_tma' are used from bdaily. The bdaily dictionary may be provided by sl_tma() function.
The input parameter 'mindu' determines the minimum d.u. value to apply the correction to 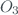 and
and  , as shown above. By default this parameter takes a value of 5.
, as shown above. By default this parameter takes a value of 5.
This function returns the input measure structure, adding the following fields, calculated as described above: 'o3_sl', 'so2_sl', 'o3_slcor' and 'so2_slcor'.
uv_cal()
This function computes the UV irradiance and DUV (Diffey-weighted UV irradiance). UV irradiance is calculated from UV Brewer measurements (including uv, ux, and ua) and the Brewer responsivity determined using a calibrated light source.
DUV is the Diffey-weighted UV irradiance, or erythemal dose rate.
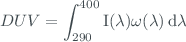
Where 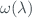 is the erythemal action spectrum defined as:
is the erythemal action spectrum defined as:
![Equation \begin{displaymath}
\[ \omega(\lambda) =
\begin{cases}
1 & \quad \text{if } 290 < \lambda \leq 298 \\
10^{0.094(298-\lambda)} & \quad \text{if } 298 < \lambda \leq 329 \\
10^{0.015(139-\lambda)} & \quad \text{if } 329 < \lambda \leq 400 \\
0 & \quad \text{if } \lambda < 400 \\
\end{cases}
\]
\end{displaymath}](/dokuwiki/lib/exe/fetch.php?media=wiki:latex:/img3fe5c1570e6d54a68d89e7095c1d21d1.png)
A correction is included in the erythemal action spectrum to account for the interval up to 400nm not measured by the Brewer.
DUV value is typically up to 250 mW/m². It can be arbitrarily divided by 25 mW/m² to generate the UVI (Ultraviolet index), which takes values from 0 to 11, although it can reach higher values.
Example
brewer.uv_cal(uv,uvr)
This function returns the input uv structure, adding the 'irradiance' and 'duv' fields.
Control
| Function | Short Description |
|---|---|
| check_hg() | Returns a list with the HG flags. |
| sl_dailymedian() | Returns the daily median double ratio of SL. |
| sl_tma() | Returns the triangular moving average double ratio of SL. |
| temp_filter() | Returns a filtered list of measurements based on the temperature. |
| gmt_filter() | Returns a filtered list of measurements based on the time (GMT). |
| outliers_filter() | Returns a list of measurements removing outliers. |
| measure2summary() | Returns the summary everaging in a list of measurements. |
| tempfit() | Returns the linear regression between instrumentally corrected measurements and temperature. |
| tempanalysis() | Compares results for old, new and zero temperature coefficientes. |
check_hg()
This function computes a list of flags with True/False values. The flag will be True for a Brewer measurement if the difference between the calculated micrometer step position during mercury-line wavelength calibration and the value saved during the installation is less than hglimit steps for the two HG measurements made before and after the Brewer measurement. Otherwise the flag will be False.
Example
brewer.check_hg(mesl,hgl,config,hglimit=1)
mesl and hgl are lists of measure and hg dictionaries respectively. The field 'gmt' is used from measure, the fields 'gmt' and 'step2' are used from hg, and the filed 'wstepn' is used from config.
The input parameter 'hglimit' determine the maximum allowed difference between 'step2' and 'wstepn'. By default this parameter take a value of 1.
This function returns the a list of True/false values.
sl_dailymedian()
This function calculates the median value of 'double_ratio1' and 'double_ratio2' for a day.
Example
brewer.sl_dailymedian(sll,bdaily)
sll is a lists of measure dictionaries. The fields 'gmt', 'double_ratio1' and 'double_ratio2' are used from measure. If input sll list is void, a ValueError is raised. Optionally, a bdaily dictionary can also be pass to the function to be used in the output.
This function returns a bdaily dictionary with the fields 'date', 'sl_r5_median', 'sl_r6_median' and 'sl_num'.
sl_tma()
This function applies a triangular moving average over the daily median values of 'double_ratio1' and 'double_ratio2', in a window of 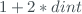 days (seven days by default) are used.
days (seven days by default) are used.
Example
brewer.sl_tma(date,bdailyl,dint=3)
The input parameter date is a python date object. bdailyl is a lists of bdaily dictionaries. The fields 'date', 'sl_r5_median', 'sl_r6_median' are used from bdaily. If the intersection between the input bdailyl list and the window is void, a ValueError is raised.
This function returns a bdaily dictionary for the 'date' day with the new fields 'sl_r5_tma', 'sl_r6_tma' and 'sl_num_tma'. If there is not a bdaily dictionary in the bdailyl list for 'date' day, 'sl_num' filed is set to 0 and 'sl_r5_median' and 'sl_r6_median' are set to None.
temp_filter()
This function returns a filtered list of measurements based on the temperature. It accepts two input parameters: 'mlinput' and 'temp_range'.
- 'mlinput' is a list of measurements ds, sl, etc.
- 'temp_range' is a list of 0,1 or 2 temperature values (floats). If 'temp_range' has zero values nothing is done. If it has one temperature value, the function returns the measurements with 'temp' values greters or equal to temp_range[0]. If it has two temperature values, the function returns the measurements with 'temp' values betwen temp_range[0] and temp_range[1].
Example
import datetime import brewer import brewerjson brewerid=185 user='user' password='password' date1=datetime.date(2012,2,7) ds=brewerjson.getDataList(brewerid,user,password,"DS",date1) dsf = brewer.temp_filter(ds,[20])
gmt_filter()
This function returns a filtered list of measurements based on the time (GMT). It accepts two input parameters: 'mlinput' and 'gmt_range'.
- 'mlinput' is a list of measurements ds, sl, etc.
- 'gmt_range' is a list of 0, 1, 2 or 4 datetime values. If 'gmt_range' has zero values nothing is done. If it has one value, the function returns the measurements with 'gmt' values greter or equal to gmt_range[0]. If it has two values, the function returns the measurements with 'gmt' values between gmt_range[0] and gmt_range[1]. If it has four values, the function returns the measurements with 'gmt' values between the interval gmt_range[0] and gmt_range[1] or between the interval gmt_range[2] and gmt_range[3].
Example
import datetime import brewer import brewerjson brewerid=185 user='user' password='password' date1=datetime.date(2012,2,7) ds=brewerjson.getDataList(brewerid,user,password,"DS",date1) dsf=brewer.gmt_filter(ds,[datetime.datetime(2012, 2, 7, 12, 0, 0),datetime.datetime(2012, 2, 7, 15, 0, 0)])
outliers_filter()
This function returns a filtered list of measurements removing outliers. It is considered as outliers all measurement which are more than alpha standard deviations away from the mean on either channel ('raw_counts_w0',…,'raw_counts_w5').
The function accepts two input parameters:
- 'mlinput' is a list of measurements ds, sl, etc.
- 'alpha' is a float number. By default 'alpha' value is 3.
Example
import datetime import brewer import brewerjson brewerid=185 user='user' password='password' date1=datetime.date(2012,2,7) ds=brewerjson.getDataList(brewerid,user,password,"DS",date1) dsf=brewer.outliers_filter(ds,3)
measure2summary()
This function returns a list of averaged measurements to reproduce the brewer summaries from individual data, using 'n_summary' to group the measurements.
The function accepts only an input parameters:
- 'meslist' is a list of measurements ds, sl, etc.
Example
import datetime import brewer import brewerjson brewerid=185 user='user' password='password' date1=datetime.date(2012,2,7) ds=brewerjson.getDataList(brewerid,user,password,"DS",date1) ds=brewer.airmass_calcl(ds,config) ds=brewer.instrumental_corl(ds,config) ds=brewer.rayleigh_corl(ds,config) dss=brewer.measure2summary(ds)
tempfit()
This function does 8 linear regressions between instrumentally corrected measurements ('measure_w0',…,'measure_w5','double_ratio1' and 'double_ratio2') and temperature.
The function accepts two input parameters:
- 'mlinput' is a list of instrumentally corrected measurements ds, sl, etc.
- 'alpha' is a float number used to remove outliers during linear fit. After a first linear regression, residuals are calculated and removed all measurement which residuals are more than alpha times the standard deviation of the residuals. The process is repeated until no outlier is removed. By default 'alpha' value is 0 and no iteration is done.
tempfit function returns a dictionary with 8 elements 'w0', 'w1 “,” w2 “,” w3 “,” w4 “,” w5 “,” R5 “and” R6', each containing the values of a (slope), sa (standard deviation of a), b (intercept), sb (standard deviation of b), r2 and res (residual list) of the 8 linear regression. In addition the following data is returned:
- 'tmax' = maximum temperature
- 'tmin' = minimum temperature
- 'tnum' = number of different temperature values
- 'olnum' = number of outlayers
- 'itnum' = number of iterations performed (if alpha > 0 the linear adjustments are repeated until no outlayers)
- 'measure' = data used in the linear fit after eliminating the aoutlayers.
Example
import datetime import brewer import brewerjson brewerid=185 user='user' password='password' date1=datetime.date(2012,2,7) date2=datetime.date(2012,2,8) sl=brewerjson.getDataList(brewerid,user,password,"SL",date1,date2) config=brewerjson.getDataList(brewerid,user,password,"ConfigbyDate",date1,date2) sl=brewer.instrumental_corl(sl,config) fit=brewer.tempfit(sl,alpha=3)
tempanalysis()
This function calculate new temperature coefficients or apply the temperature coefficients passed as function parameters. It calculate data for 'old', 'zero' and 'new' temperature coefficients. The output of the tempanalysis() function is a dictionary which includes:
- 'old' is a dictionay with data from temperature fit when old temperature coefficients are applied
- 'zero' is a dictionay with data from temperature fit when zero temperature coefficients are applied
- 'new' is a dictionay with data from temperature fit when new calculated temperature coefficients or passed as function parameter are applied.
- 'F1avg' is a list with the daily average of the first channel raw intensity for the first channel ('raw_counts_w1')
- 'F1mean' is the average of the daily values 'F1avg'
- 'F1std' is the standard deviation of the daily values 'F1avg'
- 'R5conf' is alist with the refence values for R5 in the config data
- 'R6conf' is alist with the refence values for R6 in the config data
Each element old, new and zero is a dictionary which includes:
- 'tcoef' is a list of temperature coefficients
- 'fit' is a dictionary with information of temperature fit (output of tempfit() function)
- 'measure' is a dictionary with the data used for the temperature fit
- 'config' is a dictionary with the config data used for the temperature fit
- 'R5avg' is a list with the daily average of the 'double_ratio1' when the correspondig temeprature coefficients are applied
- 'R5mean' is the average of the daily values 'R5avg'
- 'R5std' is the standard deviation of the daily values 'R5avg'
- 'R6avg' is a list with the daily average of the 'double_ratio2' when the correspondig temeprature coefficients are applied
- 'R6mean' is the average of the daily values 'R5avg'
- 'R6std' is the standard deviation of the daily values 'R5avg'
The function accepts four input parameters:
- 'slinput' is a list of dictionaries with SL measurements
- 'configinput' is a list of dictionaries with brewer configurations
- 'ntc' is a list of new temperature coefficients. If ntc=[], the function calculates the new temperature coefficients.
- 'alpha' is a float to set the outlayer filter in tempfit function
Example
import datetime import brewer import brewerjson brewerid=185 user='user' password='password' date1=datetime.date(2012,2,7) date2=datetime.date(2012,2,8) sl=brewerjson.getDataList(brewerid,user,password,"SL",date1,date2) config=brewerjson.getDataList(brewerid,user,password,"ConfigbyDate",date1,date2) ta=tempanalysis(sl,config,[],0) ta.keys()
Astronomical
| Function | Short Description |
|---|---|
| solar_ha_dec_et() | Returns the solar hour angle, declination and equation of time. |
| solar_zenith_angle() | Returns the solar zenith angle. |
| solar_azimuth_angle() | Returns the solar azimuth angle. |
| moon_ha_dec() | Returns the moon hour angle and declination. |
| moon_zenith_angle() | Returns the moon zenith angle. |
| moon_azimuth_angle() | Returns the moon azimuth angle. |
| min_sza() | Returns the minimum solar zenith angle (maximum elevation). |
| sza_to_time() | Returns the times at wich solar zenith angle is achieved for a specific day. |
| apparent_zenith_angle() | Returns zenith angle of the sun/moon corrected by refraction, also known as apparent zenith angle. |
solar_ha_dec_et()
This function returns the solar hour angle, declination and equation of time for a specific day at a specific location. In this case only geographic longitude is required to specify the location. The method used to calculate these parameters is the same as that implemented in the Brewer operative software (Tom McElroy / Volodya Savastiok).
Example
brewer.solar_ha_dec_et(datet, lon)
The input parameter datet is a python datetime object. lon is a float that represents the geographic longitude in degrees.
The solar_ha_dec_et() function returns a tuple with tree elements: hour angle in radians, solar declination in radians and equation of time in minutes.
solar_zenith_angle()
This function returns the solar zenith angle for a specific day at a specific location. The method used to calculate these parameters is the same as that implemented in the Brewer operative software (Tom McElroy / Volodya Savastiok).
Example
brewer.solar_zenith_angle(datet, lat, lon)
The input parameter datet is a python datetime object. lat and lon are floats that represents the geographic latitude and longitude in degrees respectively.
The solar_zenith_angle() function returns a float with the value of the solar zenith angle in degrees.
solar_azimuth_angle()
This function returns the solar azimuth angle for a specific day at a specific location. The method used to calculate these parameters is the same as that implemented in the Brewer operative software (Tom McElroy / Volodya Savastiok).
Example
brewer.solar_azimuth_angle(datet, lat, lon)
The input parameter datet is a python datetime object. lat and lon are floats that represents the geographic latitude and longitude in degrees respectively.
The solar_azimuth_angle() function returns a float with the value of the solar azimuth angle in degrees.
moon_ha_dec()
This function returns the moon hour angle and declination for a specific day at a specific location. In this case only geographic longitude is required to specify the location. The method used to calculate these parameters is the same as that implemented in the Brewer operative software (Tom McElroy / Volodya Savastiok).
Example
brewer.moon_ha_dec(datet, lon)
The input parameter datet is a python datetime object. lon is a float that represents the geographic longitude in degrees.
The moon_ha_dec() function returns a tuple with two elements: hour angle in radians and moon declination in radians.
moon_zenith_angle()
This function returns the moon zenith angle for a specific day at a specific location. The method used to calculate these parameters is the same as that implemented in the Brewer operative software (Tom McElroy / Volodya Savastiok).
Example
brewer.moon_zenith_angle(datet, lat, lon)
The input parameter datet is a python datetime object. lat and lon are floats that represents the geographic latitude and longitude in degrees respectively.
The moon_zenith_angle() function returns a float with the value of the moon zenith angle in degrees.
moon_azimuth_angle()
This function returns the moon azimuth angle for a specific day at a specific location. The method used to calculate these parameters is the same as that implemented in the Brewer operative software (Tom McElroy / Volodya Savastiok).
Example
brewer.moon_azimuth_angle(datet, lat, lon)
The input parameter datet is a python datetime object. lat and lon are floats that represents the geographic latitude and longitude in degrees respectively.
The moon_azimuth_angle() function returns a float with the value of the moon azimuth angle in degrees.
min_sza()
This function returns the minimum solar zenith angle (maximum elevation) for a specific day at a specific location. This is calculated considering the solar hour angle is zero.
Example
brewer.min_sza(d,lat,lon)
The input parameter datet is a python datetime object. lat and lon are floats that represents the geographic latitude and longitude in degrees respectively.
The min_sza() function returns a float with the value of the minimum solar zenith angle in degrees.
sza_to_time()
This function returns the times at which solar zenith angle (SZA) is achieved for a specific day. If the input SZA is lower than the SZA at noon, the function rise an ValueError showing the message “The solar zenith angle is not achieved on the input day.
This function allows us to compute sunrise and sunset times by introducing SZA=0. To compute noon time we can use the SZA value retrieve by min_sza() function.
Example_
brewer.sza_to_time(sza,d,lat,lon)
The input parameter sza is a float (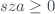 ) that represent solar zenith angle in degrees. d is a python date object. lat and lon are floats that represents the geographic latitude and longitude in degrees respectively.
) that represent solar zenith angle in degrees. d is a python date object. lat and lon are floats that represents the geographic latitude and longitude in degrees respectively.
The sza_to_time() function returns a tuple with two datetime objects, with the times when the sun reaches the input zenith angle during the morning and in the afternoon. If input sza is not achieved on the input day, a ValueError is raised.
apparent_zenith_angle()
This function returns the solar/moon apparent zenith angle, that is, the zenith angle considering atmospheric refraction. The method used to calculate this parameter is the same as that implemented in the Brewer operative software (Tom McElroy / Volodya Savastiok), and is described in Archer - 1980 - Comments on “Calculating the position of the sun”. The correction is only applied if 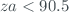 .
.
Example
brewer.apparent_zenith_angle(za)
The input parameter za is a float that represent solar/moon zenith angle in degrees.
The sza_to_time() function returns a float with the corrected azimuth angle in degrees.
Airmass
| Function | Short Description |
|---|---|
| brewer_airmass() | Returns the air mass calculated for a delta layer at a fixed altitude. |
brewer_airmass()
This function returns the air mass calculated for a delta layer at a fixed altitude, as is described in Brewer MkIII - Operator's Manual:

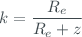
where 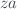 is a the zenith angle,
is a the zenith angle,  is the delta layer height, and
is the delta layer height, and 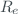 = 6370 is the radius of earth in km.
= 6370 is the radius of earth in km.
This function is typically used considering a layer at an altitude of 22 km for ozone air mass, and a layer at an altitude of 5 km for Rayleigh air mass.
Example
brewer.brewer_airmass(za,z)
The input parameter 'za' is a float with the solar/moon zenith angle in degrees. 'z' is a float that represents the layer height in km.
The brewer_airmass() function returns a float with the air mass value.
Data Reduction
| Function | Short Description |
|---|---|
| darkcount_cor() | Returns a list with the dark count corrected measurements. |
| deadtime_cor() | Returns a list with the dead time corrected measurements. |
| temp_cor() | Returns a list with the temperature corrected measurements. |
| attenuation_cor() | Returns a list with the filter attenuation corrected measurements. |
darkcount_cor()
This function subtracts the dark count from raw data, then scales the result to produce count rates, in counts per second:
![Equation \begin{displaymath}
f_{out}[i] = \frac{2*(f[i]- dark )}{cycles*it}
\end{displaymath}](/dokuwiki/lib/exe/fetch.php?media=wiki:latex:/img439123daa85474da2a36290026b15d8c.png)
Example
brewer.darkcount_cor(f,dark,cycles,it)
The input parameter f is a list of five integers with the raw measurements. dark is a float with the dark count value. cycles is an integer with the number of cycles for each measurement. it is a float with the slit sampling time.
The darkcount_cor() function returns a list with the dark count corrected measurements in counts per second.
deadtime_cor()
This function compensates for the dead time, assuming a Poisson distribution function of a paralyzable detection system. The method iterates 9 times the equation:
![Equation \begin{displaymath}
f_{out}[i] = f[i] * e^{f_{out}[i]*t1}
\end{displaymath}](/dokuwiki/lib/exe/fetch.php?media=wiki:latex:/img111749cfc1118023c0b56cd65b159acb.png)
The deadtime-compensated count rates are normalized by computing the base ten logarithm of e, then scaled by 10000, thus allowing integer arithmetic.
This function is typically applied after dark count correction.
Example
brewer.deadtime_cor(f,t1)
The input parameter f is a list of five floats with the measurements. t1 is a float with the deadtime of the photon-counting system.
The deadtime_cor() function returns a list with the dead time corrected measurements in counts per second.
temp_cor()
This function compensates for temperature-dependent characteristics of the spectrometer assembly:
![Equation \begin{displaymath}
f_{out}[i] = f[i] + (tc[i] * t)
\end{displaymath}](/dokuwiki/lib/exe/fetch.php?media=wiki:latex:/imgbabeeddbd2de82b4b405998202db84af.png)
This function is typically applied after dead time correction.
Example
brewer.temp_cor(f,t,tc)
The input parameter f is a list of five floats with the measurements. tc is list of five floats with the temperature coefficients. t is a float with the temperature of the system in Celsius degrees.
The temp_cor() function returns a list with the temperature corrected measurements in counts per second.
attenuation_cor()
This function compensates for attenuation of the neutral-density filters used to adjust the light level entering the spectrometer:
![Equation \begin{displaymath}
f_{out}[i] = f[i] + af[fp]
\end{displaymath}](/dokuwiki/lib/exe/fetch.php?media=wiki:latex:/img18a5eb2386f3ba48218d4d703a75b6f7.png)
This function is typically applied after temperature correction.
Example
brewer.attenuation_cor(f,af,fp)
The input parameter f is a list of five floats with the measurements. taf is list of six floats with the attenuation values of the neutral-density filters. fp is an integer with the filter position.
The attenuation_cor() function returns a list with the attenuation corrected measurements in counts per second.
Auxiliary Functions
| Function | Short Description |
|---|---|
| wsum() | Returns the weighted sum from all measurements on a list. |
| weeknum() | Returns the weighted sum from all measurements on a list. |
| weektodate() | Returns the weighted sum from all measurements on a list. |
wsum()
This function computes the sum of products over two lists. Both input lists should have the same length:
![Equation \begin{displaymath}
wsum=\sum_{i}f[i]*w[i]
\end{displaymath}](/dokuwiki/lib/exe/fetch.php?media=wiki:latex:/img62133f25fb6fae862cac3b3d437dc268.png)
Example
import brewer f=[1,2] w=[2,3] brewer.wsum(f,w)
The input parameter f is a list of floats. w is list of of floats of the same length than f.
The wsum() function returns a float with the weighted sum value.
weeknum()
This function calculate the week number of year. It is based in the matlab function of the same name.
The function accepts three input parameters:
- 'd' is a date
- 'w' is an integer repressenting the week start value (Sunday:1, Monday:2, Tuesday:3, Wednesday:4, Thursday:5, Friday:6, Saturday:7)
- 'e' is a bool to use or not use European standard
Example
import brewer brewer.weeknum(datetime.date(2015,1,5),1,False)
weektodate()
This returns a tuple with the first and last days of acertain week.
The function accepts four input parameters:
- 'n' is an integer representing the week number
- 'yrs' is an integer representing the year
- 'w' is an integer repressenting the week start value (Sunday:1, Monday:2, Tuesday:3, Wednesday:4, Thursday:5, Friday:6, Saturday:7)
- 'e' is a bool to use or not use European standar
Example
import brewer brewer.weektodate(2,2015,1,False)